Physical resemblance to real-life characters is not always an issue for the casting of Hollywood’s movies, especially when the protagonist has a less known name to the general public. There have been over time a small number of movies featuring a real scientist at the center of the storyboard, and resemblance does not seem to have been the main concern for the production. Let’s just forget the too charming Greer Garson in the too tight clothes of Madame Curie. But then, the muscular Russel Crowe in A Beautiful Mind did not bear even the smallest resemblance to the slim John Nash. Neither Aidan Mc Ardle, nor Vincenzo Amato were decent stand-ins for Albert Einstein (not enough to put on a moustache and scruff your hair…). And most certainly, Michael Sheen and Lizzy Caplan were not chosen to interpret the couple Masters and Johnson because of their physical resemblance to the originals. Maybe a more honest attempt was Eddie Redmayne playing Stephen Hawking in The Theory of Everything, probably because Hawking was already too well known to the public. By general consensus, the best example should be the excellent Benedict Cumberbatch in The Imitation Game, who indeed had some similarity to the facial traits of Alan Turing. Despite the many flagrant inaccuracies of the movie script, however, he portrayed in the best possible way the oddness, eccentricity, emotional conflict, and tragic sides of Turing’s character (as publicly acknowledged by surviving members of Turing’s family).
In the movie, Alan Turing is seen as a master code-breaker and cryptographer, completely focused on the design of a machine of unique capability, engaged in the decryption of the German Enigma war codes. For the benefit of the public, the great mathematician is there represented as a solitary genius, working in isolation against many enemies that oppose his views, and assembling the huge electro mechanical computer, with hundreds of wheels and cranks, almost by himself. This is utterly far from the reality of what was going on in Bletchey Park during the war years. Construction of the “Victory” machine (rebranded “Christopher” in the movie) was a collaborative, not an individual effort. It was a British Bombe machine, partly inspired by a design due the Polish cryptanalyst Marian Rejewski, from the Polish Cypher Bureau, who had conceived a machine in 1938, called bomba kryptologiczna. The new English machine in Bletchey was just the first of about 200 copies built during the final war years, and the major contribution to its design was actually due to another great British mathematician, Gordon Welchman (not mentioned in the film). Moreover, the movie hints at a major contribution of Turing also in creating the Colossus machine, the first digital computer using thermionic valves, which was actually assembled at Bletchey Park in 1943, but in which Turing had no part.
So, by now Alan Turing has passed in the popular culture as a solitary wizard computer builder and cryptography guru, as well as for his singular suicide with the Snowwhite poisoned apple. In reality he was not so much of a solitary character, and for a large part of his life he was a theorist in the discipline of computer science, which then was just in its infancy, and for which he is properly acknowledged as one of the founding fathers. In 1945-47 he actually laid out the design for the ACE, Automatic Computing Engine, the first complete specification of a stored-memory computer. A pilot version of ACE was built in Cambridge in 1950, and several computers of those days owe much to the early design of Turing; however, a complete ACE was built only after Turing’s death. In 1949, after being appointed reader in mathematics at the Victoria University in Manchester, Turing was nominated director of the Computing Machines Laboratory, where he continued working on programming models and rather abstract problems in computing theory, including one of the earliest computing models of a chess game (he tried to actually run this code on a Ferranti Mark-1 computer in 1952, but the computer nearly blew up because of excess power absorption).
I first came to know Turing’s work because of a 1984 essay in Scientific American describing the “universal Turing machine”, his most important work (ignored by the movie, but likely deserving a Nobel prize or Fields medal). In 1936, just fresh from his undergraduate degree at the King’s College of London, of which he had been elected fellow since a few months, Turing published in the Proceedings of the London Mathematical Society a two-part work, “On Computable Numbers”. Undoubtedly the most famous paper in the history of computing, this work is a mathematical description of an imaginary computing device, designed to replicate the mathematical “states of mind” and symbol-manipulating abilities of a human computer. Turing conceived the universal machine as a means of answering the last of the three questions about mathematics posed by David Hilbert in 1928: is mathematics complete; is mathematics consistent; and is mathematics decidable. Hilbert’s final question, known as the Entscheidungsproblem, concerns whether there exists a definite method that can be applied to any mathematical assertion, to decide whether that assertion is true. Kurt Gödel in 1930 had already shown that arithmetic (and by extension mathematics) is both inconsistent and incomplete. Turing showed, by means of his universal machine, that mathematics is also undecidable. Like an ordinary typewriter (I am sorry if many of you, younger readers, have never seen one), the Turing machine can be imagined of being composed of a movable head that prints symbols on a tape that, for convenience, is assumed to be divided into discrete segments, and of practically infinite length. The head can move left or right by one segment at each time, and it can perform the elementary actions of printing a symbol, erasing it, or read it. The machine’s activity is rigorously determined by a three-parts instruction at each step: the first part designates the symbol to leave at the current location (hence the machine reads it, and compares it with the one in the instruction); the second part specifies the state of the machine at the next step; and the third part tells the machine to make the next move either left or right. Given such an extremely simple set up, Turing proved that his ideal machine could perform any conceivable computation that was representable by a finite algorithm (but please do not ask how fast). And, most importantly, he proved that there is no way to decide if whether the machine will ever halt, for any given algorithm. That nailed Hilbert’s third question. With his PhD, obtained at Princeton in 1938, Turing completed his ideal machine by adding the oracles (this one and the related ‘Turing reduction’ are very interesting points, but I will stop here for the sake of keeping today’s story within acceptable lengths).
The second key contribution of Alan Turing to our modern world came with the paper “Computing machinery and intelligence” (Mind, 49 (1950) 433-460), which defined the “Turing test”. The movie ignores also this aspect, but takes it for the title (“imitation game” was the definition Turing originally gave to his test). The paper opens with the sentence: “I propose to consider the question, Can machines think?“, and that already says it all. Turing then describes a simple game involving three players: two unknowns A and B, and C in the role of an interrogator. C is unable to see either A or B, and can communicate with them only through written notes. In the modern version of the test, either A or B are replaced by a computer, and C tries to determine which of the two is the man and which is the machine. There have been a number of improvements of the original test, since in its first version several key points were left open (for example, does C know for sure that one of A or B is a computer, or he is completely unaware of the possibility?). However, even if imperfect, Turing’s test goes at the heart of a very modern question, since neither the philosophy of mind, psychology or neuroscience have been able to provide definitions of “intelligence” and “thinking” that are sufficiently precise and general to be applied to machines. Without such definitions, the central questions posed by the development of artificial intelligence cannot be answered. The Turing test is the attempt at providing a pragmatic answer, while it does not directly test whether a computer behaves intelligently. In fact, it tests only whether the computer behaves like a human being, or more generally, whether the computer deliberately imitates a human being, this latter being an even more intriguing question.
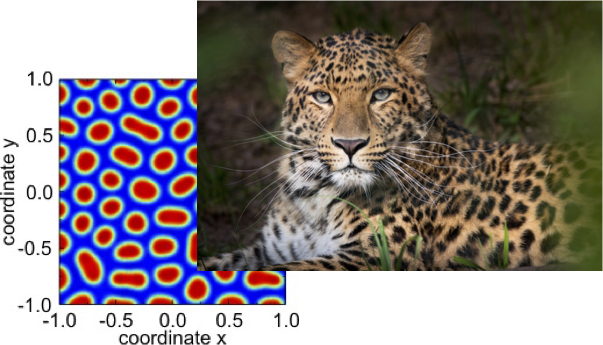
But the reason why I am writing today about Turing is neither his ideal machine, nor his ideal test. Seventy years ago, in 1952, he published a landmark work in theoretical biology that should have granted him another Nobel prize (this time in medicine, maybe). With the paper “The chemical basis of morphogenesis” (Phil. Trans. Roy. Society London B237 (1952) 37-72) he created and entirely new scientific field from scratch. With this work, Turing proposed a mathematical theory of biological morphogenesis to explain the emergence of spatial organization in the embryo. The original model consisted of two molecular species (‘morphogens’, a term he coined anew) that diffuse through the embryonic tissue, and chemically react with each other. He proved that, under certain conditions, such a simple two-component reaction-diffusion system should be able to spontaneously create periodic patterns in space, such as dots and stripes in animal furs or fishes’ skin. The idea that a self-organized symmetry breaking of molecular concentrations would be driven by diffusion was counterintuitive, as diffusion normally has the opposite effect of smoothing spatial heterogeneities, and rather tends to generate uniform distributions. The model was initially difficult to accept, mostly because of the lack of conclusive evidence of real-world examples, for almost 40 years after Turing proposed it. Firstly, in its original form, a ‘Turing system’ requires two chemical species that diffuse at significantly different rates, whereas in reality many species that might conceivably form patterns have very similar diffusion rates. Secondly, there appeared to be only extremely narrow ranges of the reaction parameters that would be compatible with a Turing pattern; generating a pattern would, therefore, require setting these parameters with unrealistic precision. Turing patterns seemed an unlikely and intrinsically not robust phenomenon. But progressively, fitting examples have been found both in chemistry and embryology, also involving combinations of more than just two species, and the influence of this ground-breaking theory has been phenomenal, as it has subsequently been invoked to explain patterning processes in chemical reactions, nonlinear optical systems, semiconductor nanostructures, galaxies, predator-prey models in ecology, vegetation patterns, cardiac arrhythmias, and even crime spots in cities.
A key point in creating a pattern is the instability that leads to a bifurcation in the mathematical equations for the concentrations, and is coupled to their spatial distribution. Two papers (among many) appeared just a few weeks ago, have applied Turing’s model of pattern formation in the context of COVID-19 spreading, to study the diffusion of the susceptible and infected (that is, the two diffusing-reacting species) in the periodic behavior of the disease, within a network-organized system of nodes that could represent connectivity between urban sites (Physica A603 (2022) 127765; Europhys. Lett. 137 (2022) 42002). Epidemiological deterministic models, like the Susceptible–Infected–Recovered (SIR) model, have been widely employed in the past two years to model and predict COVID-19 spreading. The original analysis in the two cited papers, characterizing the different classes of people in the system (a city, region, country) as reacting-diffusing species, allowed to highlight the role of network parameters (connectivity rate, infection rate, infection concentration, etc.) on the outbreak of an infectious disease. Given that the stability of the network-based SIR model is linked to the eigenvalues of the network matrix (specifically, to the maximum eigenvalue), a ‘Turing instability’ coupling the network connection rate and infection rate was found to be able to predict the spread of the infection and its periodic recurrence (pattern formation), using data from COVID-19 to validate the results.
Similar works translating the Turing mechanisms from continuous manifolds to discrete networks have become increasingly popular. The SIR epidemic model described in the two papers above, and others in many different studies, actually treats a symmetric network, a choice which makes the Laplacian (the matrix of second derivatives of the diffusion term) diagonalizable, and makes the detection of the instability rather obvious. However, interest is now raised also in directed networks, for which the connectivity between two nodes is asymmetric (ij≠ji), and the matrix is not diagonalizable. This latter case is very interesting, since different paths in such a network are not equivalent, and the system becomes explicitly time-dependent (paths have a time arrow), with possible applications ranging, e.g., from the synchronization of synaptic couplings in the brain, to the directional organization of links in social networks like Twitter or Facebook.
Turing patterns have gone a long way in these seventy years.
