Despite its pretty vulgar use as the place where food for the family is prepared, kitchen as you know is a very nice place to do physics experiments. In this periodic letter, I already described the physics of coffee making, the phase equilibrium of ice cream, soap bubbles in the freezer, the twist in spaghetti breaking, and the growth of giant pumpkins. Today I want to talk about kitchen vortices (and in the bathroom as well).
Concentrated vortices are fascinating and highly complicated flow phenomena, which have been studied for centuries in the contexts of nature and technology. The classic, free-surface draining vortex, the so-called “bathtub” vortex, is maybe the best known, with its familiar depression of the surface accompanied by rotating ripples, and the distinct appearance of a “swirl” (adding the – way too tiny – effect of Coriolis force has propagated the wrong belief that the vortex in the bathtub would turn in opposite ways in the upper vs. northern emispheres… more on that below). But if we could look beneath the water surface, we would see an intricate assembly of space- and time-dependent three-dimensional flow processes, which still lack a complete scientific elucidation.
Key insights in the physics of fluids are often captured by dimensionless numbers, expressing the ratio between antagonist forces or energy dissipation components. One of the best known is the Reynolds number, Re=ρvL/μ, expressing the ratio between inertial and viscous forces in a fluid that is subject to a non-uniform internal velocity field. The numerator is the product of the density ρ (mass/volume), the fluid velocity v, and a characteristic length L; the denominator is the dynamic viscosity μ of the fluid (force x time /surface). If we imagine a nice and warm carrot and onion soup in a cylindrical pot, hand-stirred by a ladle of size L rotating with an angular speed ω (rad/second), the fluid velocity about the ladle is roughly v=ωL; the dynamic viscosity depends strongly on the temperature, for a pot of vegetable soup cooking at 80-100oC it could be of a few mPa·s. Then, a rotation velocity of your ladle about 1-2 turns per second is already enough to induce a turbulent flow (Re>104). As such, a free-surface vortex can result, as from any natural or artificial circulation field that generates a strong tangential velocity field vt. Upon a closer look, however, it can be observed that a more complex secondary flow field is established in the pot of soup, also comprising a radial vr , and an axial velocity field vz in the cylinder, which are necessary for ensuring continuity of the fluid flow through the closed system.
When studying a rotating fluid, a distinction must be made between the local and global rotation of the fluid. If we imagine putting a tiny ball with a rough surface in the rotating fluid, we may observe that the ball under some conditions could start rotating about its axis. This is called the vorticity of the fluid motion, not to be confused with the global rotation of the vortex about its axis. In fact, the local rotation described as vorticity may also be opposed to the macroscopic rotation. If the fluid is rigidly rotating about the vortex axis with uniform angular velocity (so that the tangential velocity of each fluid element increases proportionally to its radial distance from the vortex center) the vorticity is the same everywhere. If, instead, the tangential velocity is inversely proportional to the radial distance, the fluid particles tend to zero vorticity and the fluid is irrotational. In general, any fluid vortex will decay to irrotational conditions once the rotational forcing is stopped. In our case, rotation conditions are imposed by the movement of the ladle in the soup. Notice that if you vigorously rotate the ladle at high speed for a few seconds, you will see that the vortex can remain in effect for quite a long time, especially if the dynamic viscosity at the denominator of Re is small (such as for a soup at water-like density). During this extra time, it is the pot walls that are providing the extra pressure to maintain the vortex, until the rotational energy is completely dissipated by internal friction.
The central empty (actually, air-filled) region of the vortex is maintained by the Bernoulli principle, according to which the faster a portion of fluid moves or rotates, the lower its potential energy and dynamic pressure. The dynamic pressure generated by the motion adds to the gravity and determines the shape of the free surface. Hence, in a rotational fluid vortex the fluid velocity is large far away from the center, and the dynamic pressure is lower close to the center: by gravity, the fluid surface tends to a concave paraboloid. You can observe this by vigorously rotating in your hands the whole pot containing the soup. At the opposite, in an irrotational fluid the velocity is higher towards the center of the vortex and decays at the periphery; the dynamic pressure should drop to infinite negative value as ρgh–K/r2 (K a force constant), but since dynamic pressure cannot be negative, it drops sharply to zero at the vortex core. The vortex free surface in this case becomes an inverted hyperboloid (Gabriel’s trumpet) with an empty hole at atmospheric pressure (ρgh) in the middle (the core). This is the case when the pot is kept still and you rotate the soup with a ladle, but can also observed in tornadoes, thanks to the condensation of water vapor by the sudden cooling imposed by the zero pressure at the inner surface, which makes visible the core of the (wet) air vortex, in some cases as large as 4-500 m with its inner volume filled with air nearly at rest, in relative calm.
A close relative of the free-surface vortex in the family of rotating flows is the classic Taylor-Couette flow of an incompressible, viscous fluid enclosed in the gap between two concentric rotating cylinders. Although the carrot and onion soup is both incompressible and viscous, it is difficult to imagine such a situation in a normal kitchen. (An empty pot rotating inside the filled one?) However, this technique is used in several food related technologies, from processing starches, making gelatins, or sterilization. Vortices can again form in the fluid comprised between the rotating cylinders when another non-dimensional number exceeds a critical value. This is the Taylor number, a combination of the ratio of cylinder rotational velocities, and the ratio of their size. In particular, when the angular velocity of the internal cylinder exceeds a critical value, a primary instability develops, and the flow becomes unstable with respect to axisymmetric perturbations. The secondary flow with radial vr and axial vz velocity components manifests itself with an arrangement of many counter-rotating vortices, stacked in the vertical direction.
An apparently similar vorticity phenomenon, however induced by adding heat as external force instead of mechanical agitation, is the formation of Rayleigh-Bénard cells in your soup, by heat convection from the bottom of the pot. With the right combination of pot height L, soup viscosity v, thermal dilatation β, and thermal diffusivity α, you may easily observe the formation of irregular cells from the surface of the soup, in which the fluid appears to rise from the center of each cell and flow down at the borders. The instability in this case is dictated by the Rayleigh number Ra=gβΔTL3/αv, and will occur upon reaching a critical temperature difference ΔT between the heated bottom and the free surface. The critical value of Ra is around 1780 for a pot with rigid bottom and open surface. For a water-like soup with β/αv ~108 s2/oCm4 the instability temperature may easily go above the boiling point of the soup, which makes the actual observation of Rayleigh-Bénard cells difficult unless you keep the soup thickness in the pot to a couple of centimeters or less.
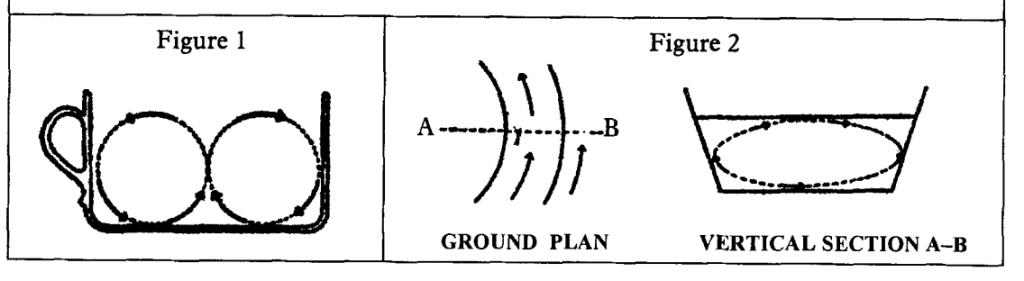
We usually stir a liquid to evenly disperse the substances in it, be it a dissolved sugar cube, or a pinch of salt, or any other solid solute. The phenomenon known as Einstein’s tea leaf paradox describes a seemingly opposite effect, in which the leaves (or other solid particles) in a well-stirred cup of tea instead become concentrated in a doughnut-shaped area, and gather at the bottom center of the cup once stirring ceases. This “paradox” has been known for nearly 200 years, and is understood to be caused as well by a secondary flow effect, induced aside of the main circular flow. It was actually James Thomson, also known as Lord Kelvin, to provide the first explanation for it, in a 1857 note to the British Association in Dublin, while studying the circulation of air currents on the Earth’s surface. At the end of his oral communication, Thomson referred just to the tea leaves in a shallow cup, as a simple example to explain his theory of atmospheric circulation. He said: “[the leaves] will collect in the centre […] carried by a current determined towards the centre along the bottom, in consequence of the centrifugal force of the lowest stratum of water being diminished […] by friction on the bottom.” So, the slowing down of water in contact with the bottom surface makes for a circular eddy that revolves the fluid from the bottom to the surface at the center, and from the surface to the bottom at the periphery. A few years later, Valentin Bousinnesq, while lecturing calculus at the Faculty of Sciences in our city of Lille, formulated the detailed theory of the formation of such secondary annular flows in 1868. But then, why it is called Einstein’s paradox?
As it turns out, Albert the Great also delivered an oral exposé, for the Prussian Academy of Sciences in Berlin, January 7, 1926. Aged almost fifty, he had already solved some of the hardest problems in physics, but he was yet keen to work also on small, forgotten questions. One of these was the so-called Baer’s Law, according to which rivers in the northern hemisphere should tend to erode chiefly on their right bank, while rivers in the southern hemisphere should do the opposite on the left bank. Again, Coriolis’ force was called in, as the explanation of this presumed north-south asymmetry, overlooking experimental verification in lieu of an unproven conjecture, and even passing the simple order of magnitude calculation that would quickly show how Coriolis’ force is about 10-5 per metre smaller than gravity, for a typical river. So, Einstein made a simple, intuitive argument to prove that, independently of the north or south, rivers erode always more on the convex side of the bend, because water velocity there is higher, and the effect of friction on the bottom makes slower water to climb in a secondary flow (perpendicular to the main flow) to the concave side, where it accumulates sediments. Hence, the river will typically become deeper at each convex side of the bends, and this effect will also force the bending radius to progressively increase, leading to the typical meandering of rivers with alternating right and left bends. And to make his case clear, also Einstein began his talk by using… the very same analogy of the cup with tea leaves accumulating in a circle at the bottom, when rotating the tea with a spoon (see the original drawing enclosed: teacup with secondary flows on the left, river cross section with convex side B and concave side A on the right). However, he did not cite his predecessor Lord Kelvin, and since then the tea leaf “paradox” remained attached to Einstein’s name. Incredibly, if you make a tour on the internet you will find a number of websites – including some universities’ – still pretending that rivers bend because of Coriolis force, and … citing Einstein’s paper in support!
