When teaching basic notions of science in schools we often make recourse to examples, analogies, similarity, even absurd schematizations. A typical example is the harmonic oscillator as a proxy for a pendulum: the former is an idealization of the latter, the analogy works pretty well in the short run, but then friction losses set in and the pendulum starts slowing down, proving to be a non-harmonic oscillator indeed. Such analogies and examples are OK, provided the teacher is able to clearly mark their limits, having at hand the more appropriate answers for those more curious students. If instead (as unfortunately too often happens) the attitude is “the actual process is not exactly like this, but the real explanation is too complicated to be given here”, the risk is that the students will soon forget the amends, and retain the wrong explanations forever. These considerations motivate the following dialog, a parody of the famous Dialogue Concerning the Two Chief World Systems by Galileo Galilei, which took place among the same three main characters, four centuries ago.
SCENE: The hall of a luxurious villa, with a balcony overlooking the river Brenta, in Veneto.
Sagredo: Dear friends, I am happy to welcome you again in my humble house, a little short of four centuries since our last meeting, when we discussed the new cosmological theories of messer Salviati. I hope we will have another interesting discussion today, in which you may expound and defend your ideas. Shall we start? What is today’s argument?
Salviati: O noble Sagredo, I am upset by the way we teach about electric currents to our students, in high schools and even in introductory university classes. Always with this terrible analogy of flowing charges alike to flowing water. However this might be useful to get the idea, such an analogy must not be taken beyond its limits, otherwise students will remain with serious misconceptions that will retard or even compromise their true understanding of the matter. For example, the resistance is akin to a water pipe squeezed at a point…? but water flux is reduced after the squeeze, electric current is not! Drifting electrons pushing each other through the wire like water molecules push each other through a pipe…? and so what about charge neutrality? And many more…
Sagredo: But then, my friend, if electrons are not being pushed to produce the current, how the energy from the battery is transmitted along the wire?
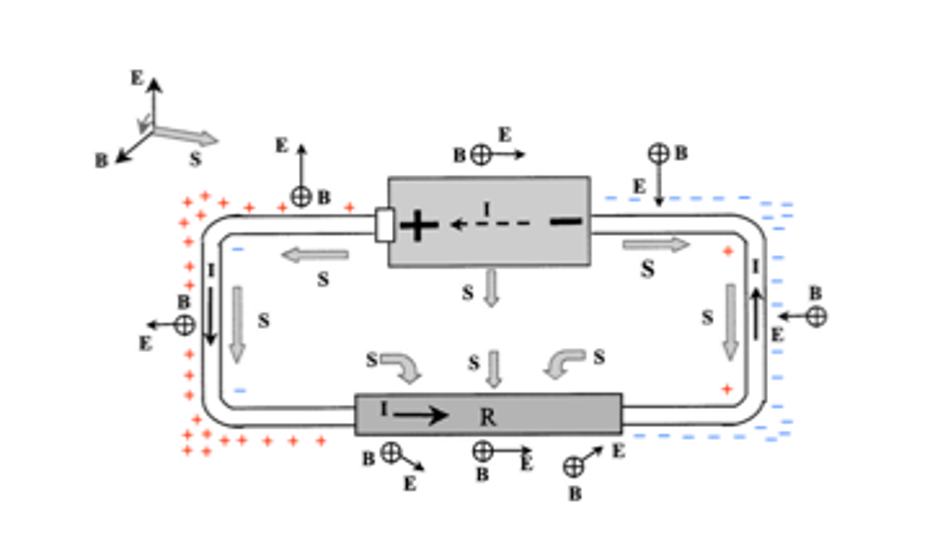
Salviati: In reality, the energy from the battery goes in the electric and magnetic fields that surround the conductor, and hence (as indicated by the famous Poynting vector S) flows into the conductor wire surface from the surrounding space, being distributed along its entire length at the speed of light.
Simplicius: (grunting) That is not possible. We know that charges are pushed along the wire by the electromotive force of the battery, and their energy is proportional to the square of the electric field parallel to the entire wire length.
Sagredo: But the Faraday principle, which I remember from my high-school studies, tells me that the electric field inside the conductor should be zero. How can that be, Simplicius?
Salviati: O noble friend Sagredo, the Faraday cage argument does not apply to the DC circuit. A Faraday cage is in electrostatic equilibrium, whereas the wire under a voltage difference is in a stationary non-equilibrium state. Our Simplicius is right in saying that there is an electric field inside the wire, parallel to its length. But he is wrong in imagining that it is the current of moving electrons that produces it. Actually, it is exactly the other way around: it is the field that produces the current, and not vice versa.
Simplicius: I cannot accept that. It is a basic physics principle that a current comes with an electric field oriented parallel to the current itself. The electric field is generated by the applied potential (as you know well, it is just the gradient of the potential) and this field gives kinetic energy to the electrons to move along the wire.
Salviati: But then, let us make a simple calculation. An electric current is the amount of charge going through a surface in some fixed time. So, the velocity is just current divided by charge density and surface area, right? For a typical metal, charge density is about 1000 coulomb per cubic cm; let us take a wire of 1 mm2 cross section, and a current of 1 amperes: we get a velocity of 0,1 cm/s. However, when you switch on your battery, the bulb lights up instantly, isn’t it…? How this would be possible, if the electrons were to carry the energy to the bulb along the wire at 0,1 cm per second?
Simplicius: I see your argument, and I am flabbergasted. But it must at least remain true that electrons receive, in some way or another, the energy from the potential drop generated by the battery, and transfer this energy along the wire up to the bulb, where this energy is used.
Sagredo: I tend to agree with our friend Simplicius in this respect. It seems odd that the battery should distribute its electric field all around the space even to infinite distances, in order to reach the bulb. The wire in some way must play a role, to guide the energy flow towards the load.
Salviati: I know that this is another problem in the education we give our students. We teach them all about the energy carried by an electromagnetic wave in vacuum, and we introduce the Poynting vector S as a very useful way to show that the energy moves in the direction perpendicular to the fields, and parallel to the wavevector. But we completely forget the S vector when we start talking about circuits. There we reason in terms of potentials and Kirchhoff’s rules, “electrokinetics” we even call it, making it seem that electromagnetic fields play no role whatsoever in circuits. You see, the wave exists in all the space simultaneously, therefore there is no problem in localizing “where” the energy goes. However, for a circuit we want to know exactly where the energy is going. Our grand spiritual father Richard Feynman was also puzzled by this problem. He made this example. Let us consider a parallel plate capacitor, slowly charged by a current. By applying Maxwell’s equations, we can see that the capacitor accumulates energy at a rate proportional to the electric field, multiplied by the time derivative of the electric field itself. Then, he asks, from which direction is the energy flowing into the capacitor?
Simplicius: What a silly question. It obviously comes injected straight from the wires.
Salviati: You are again wrong, my honorable friend. The S vector tells you whence energy comes. As you know, S is the vector product of the E and B fields. In this case, the electric field is perpendicular to the plates, while the magnetic field circulates around the axis parallel to the wires; therefore, the S vector is parallel to the plates of the capacitor. Evidently, this says that the energy comes in from all around the edges: it is not actually coming down the wires, but from the space surrounding the capacitor.
Sagredo: I am amazed. So, you are telling us that the fields established all around the space are flowing energy into the plates, and not the wires? How can that be? And what happens then for our initial example, of the current inside the conducting wire?
Salviati: Again, let us look at the S vector. Since there is a potential drop along the wire, there is also an electric field just outside the wire, parallel to the wire surface. There is, in addition, a magnetic field that goes around the wire because of the current. The fields E and B are at right angles to the wire; therefore, there is a S vector directed radially inward, into the wire lateral surface. So, there is a flow of energy into the wire from all around, equal to the energy lost in the wire as heat. Richard Feynman was himself puzzled, and called this theory “totally crazy”: electrons are getting energy because of the energy flowing into the wire from the fields in the space outside. Intuition would seem to tell us that the electrons get their energy from being pushed along the wire, so the energy should be flowing down or up along the wire. But Maxwell’s theory says that the electrons are in fact being pushed by an electric field created from some charges far away, and that the electrons get energy from these fields external to the wire. The energy somehow flows from the distant charges into a wide area of space, and then inward into the wire.
Simplicius: But then, the S vector would be changing direction with alternating currents. So, for AC currents the energy would flow alternatively in and out the wire.
Salviati: Now you surprise me, messer Simplicius! In AC current both the E and the B field are reversed at each cycle, therefore the S vector always maintains the same direction!
Simplicius: I am utterly confused. (Shakes his head in desperation) This Poynting theory seems to violate, at least partially I daresay, our intuition as to where energy is located in a conductor.
Salviati: I agree with you. But you will agree with me that energy flow is different from charge flow. Electrons do not travel at the speed of light in a conductor, they only support the electric and magnetic fields of the energetic waves. It remains unsolved, though, the microscopic charge distribution which generates the fields in the circuit.
Sagredo: That was my next question, indeed. If the conductor is everywhere neutral, where are these “distant charges” found? Maybe inside the battery?
Salviati: No, my noble friend. And I can prove it with a simple experiment. Let us start again from the simple circuit that messer Simplicius proposed, a battery connected to a light bulb by a long wire. When the switch closes the circuit, a field establishes around the wire and the bulb lights up. If this field were created by charges in the battery, then if we were to approach the battery close to the bulb by bending the wire, the bulb should get brighter. But it does not. And if we turn the battery by 90 degrees about the plane of the circuit, the electric field should be now perpendicular to the circuit, then the bulb light should go off. But it does not. There are indeed charges in the battery, but the field in the wire is not due to them.
Simplicius: (mumbling in rage) I must admit your sorcery tricks with batteries now puzzle me even more.
Salviati: The real origin of the electric field inside a long straight wire was described already 70 years ago by another spiritual grandfather of we physicists, the great Arnold Sommerfeld. He showed that the field inside the conductor is generated by charges that are accumulated at the surface of the wire. Unfortunately, we very rarely teach this concept to students, which then are led to believe a wrong explanation for the current. Such surface charges maintain the potential around the circuit; they also provide the electric field in the space outside of the conductor; and they assure the confined flow of current by adjusting the electric field parallel to the wire.
Sagredo: Surprising explanation. But why such charges would be generated in a conductor otherwise neutral?
Salviati: It is the bending of the equipotential lines of the electric field established in the conductor. The bending creates a twist in the field component perpendicular to the surface, which then must accumulate some amount of charge to compensate the discontinuity.
Simplicius: And now you are confusing me even more. You said that the surface charges create the electric field that makes the current flow in the wire; but at the same time you say that surface charges are created by bending the lines of some electric field, which therefore must already be there. (Raising his voice, infuriated) Which comes first then, the chicken or the egg?
Salviati: (smiles gently, trying to calm down S.) They indeed come both together, my friend. Initially, the electric field of the battery is just that of a finite dipole. When connected to the circuit, this electric field causes large polarization charges on the inner and outer surfaces of the wires, which move away from the poles, and accumulate at non-straight points, producing local gradients of the field. The net effect is that the electric field in the wires changes, from the initial purely dipolar field to a uniform magnitude everywhere parallel to the wire, even if you bend it in any shape you like: some charges will move on the inner and outer edges of the bend, until the additional field forces the electrons to follow the wire. This accumulation process takes place very quickly, effectively instantaneous from a macroscopic perspective.
Simplicius: I finally see your point, and cannot but convene with all your explanations. But then, what is the solution you propose? Should we start teaching our students the Maxwell’s equations already in the first year, when they have no knowledge of the necessary mathematical tools? Should we get rid of all the “old” physics and its simplified views, often found wrong or incomplete under detailed scrutiny, but still extremely useful to understand the fundamental concepts? Should we forget the great venerables Ampère, Coulomb, Ohm, Faraday, even the immense sir Isaac Newton, and begin right away with field theory, relativity and quantum mechanics? Shouldn’t we even start from high-school students, then?
Salviati: Oh no, that would be preposterous and I doubt not very useful. The problem, as I see it, is not the subjects, but the way they are taught. For example, introduce the Poynting theorem as early as possible, and show that while the electron current goes (slowly) in and out from the battery, the S vector always points toward the load on both sides of the circuit (see the drawing enclosed). This would at least clear the way by showing that energy flows always in one direction, while charges can go up or down (and also remove the ambiguity of AC vs DC currents). “Old” physics will always be there, most likely because it works so well, and because most students that are required to learn it, will only use that much physics in their life. An engineer or a biologist will probably never make use of quantum mechanics for his daily work. However, if we keep using bad analogies and wrongly constructed examples in our teaching of introductory physics, these will be the only things in physics those students will ever learn, and they will remain with such ill-formed notions forever.
Sagredo: Let us hail at the Grand Fathers of physics, then. (All the three laugh together) And let this be the final conclusion of our arguments, after which if Salviati should desire to take some interval of rest, our continuing curiosity must grant that much to him. But this is on condition that someday when it will be more convenient for him, he will return and satisfy our desires – mine in particular – regarding all the problems we further set aside. Meanwhile, according to our custom, let us go and enjoy some refreshment in the gondola that awaits us.
