Let us move for a moment on the planet Swift, orbiting around Taylor, a bright A2 class star at 380 million light years from us. Everything is solid here on Swift, except for all the living beings that are in in the form of nice, multi-colored, sweet-smelling gaseous balloons. The physicists on Swift have a tremendous mastership of quantum mechanics theory (not much different from ours), which gives them a quite solid understanding of the solid matter around them, and provides a clear understanding of their own gaseous nature. Being just a few millennia ahead of us, they have long solved the problem of quantum gravity, while they are still working hard to crack the US electoral system. Moreover, they are very happy with the Taylor-Swift greenhouse effect, which keeps their gaseous bodies at the right temperature without need to waste extra energy sources.
One day, a meteorite slams on the surface of Swift and destroys the ground in the range of kilometers. The temperature in the impact area remains very high for weeks, and the Swiftians discover that the matter at the impact site has turned into a sluggish mass, which flows here and there, impossible to contain or to manipulate. However, the first analyses show that the material is made of the very same atoms that made up the solid rock. The Swiftians, with all their beautiful theory, have no clue about the new substance that has developed with the impact, their equations give them no solution to describe its properties: it is a liquid.
As Landau swiftly (ahem…) put it: “Contrary to gases and solids, liquid thermodynamic properties and their temperature dependence can not be calculated in general form, due to the combination of strong intermolecular interactions, and the absence of the small oscillations that largely simplify solid-state theory.” A small parameter could possibly be found in liquids, but it is hidden in the liquid flow. Like in solids, liquid molecules vibrate at short times, shorter than typical relaxation times, and diffuse at long times. Phonon vibrations may give the small parameter, as in solids, but in liquids this process is short-lived. In other words, liquids may have a small expansion parameter, but you need to be very… swift to see it.
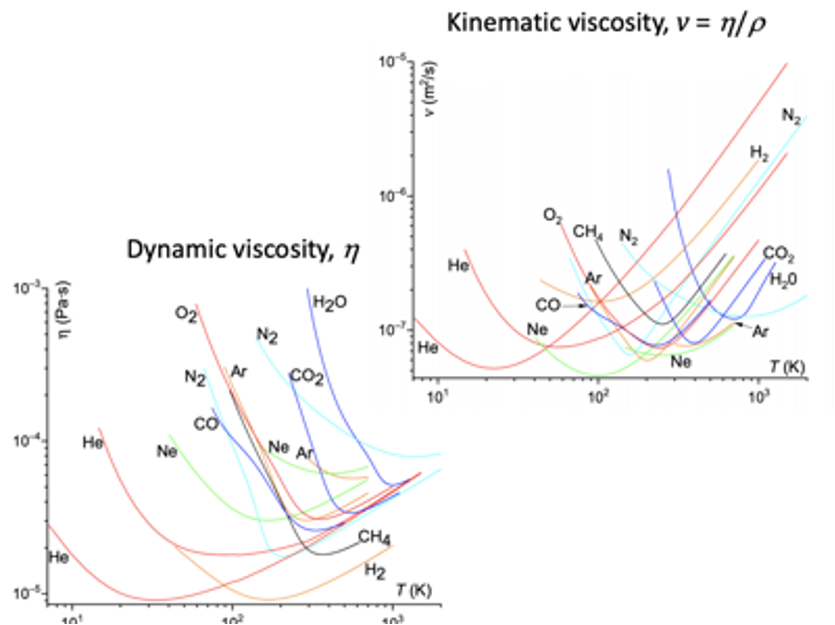
One special property of liquids is their ability to adjust, over a large interval of temperatures, the efficiency with which to transfer momentum. Macroscopically, we call this property viscosity. The dynamic viscosity (indicated by h) and the kinematic viscosity (n =h/r that is, the ratio of h to the material density r) of many materials in the fluid phase can change by orders of magnitude, by changing the temperature by just a few tens of degrees. Fluids near the glass transition can have a value of h as much as 1018 larger than that of liquid helium. However, an even more strange property of viscosity is relative to its lower limit, as Ed Purcell (recipient of the 1952 Nobel prize for the discovery of the nuclear magnetic resonance) noticed about 45 years ago, in a now famous talk that he gave during a symposium in honor of V. Weisskopf. The talk became an instant classic, because it proposed the first biophysical model of how, and most importantly why, unicellular organisms can swim [ Life at low Reynolds number, Am J Phys 45, 3 (1977) ]. However, in that same talk, Purcell noted that, while viscosities can span extremely large ranges of values, their minimum values all seem to stop around a mysterious 10-7 m2/s; and he added “I don’t understand that, that’s why I am leaving it to him [Weisskopf]”.
Calculating viscosity from theory only is a hard task, as our gaseous colleagues on the planet Swift know well. The reason is that interactions in liquids are strong and system-specific, dynamical correlations introduce long-range disorder, but maintain short-range order, so that theoretical expansions must be summed up to any order. This makes it hard to calculate viscosity parameters even in simpler fluids, with no input from some model (we could do computer simulations, but that’s another story). For molecular and network liquids, such as water, this is unworkable.
Empirically, the viscosity h of a dilute gas-like fluid is given as h =rwL/3, where r, w and L are density, average velocity of molecules and mean free path, respectively. Moreover, since L ∝ 1/r, this viscosity does not depend on the density, therefore on the pressure, and it should increase with temperature since the molecular velocity increases. On the other hand, we know that for a dense liquid, viscosity must decrease with temperature: the wax from a candle flows when we light it up, not if we put it in the refrigerator. In a simple model (Andrade), it is h=h0 exp(U/kBT), with U some activation energy. All this implies that the viscosity should have a minimum near the gas-liquid transition temperature, even more smooth for the kinematic viscosity, since the density decreases too with the temperature. However, why this minimum should be somewhat “universal” (see the enclosed figure) is unexplained.
Now, two Russian scientists, Kostja Trachenko and Vadim Brazhkin, have found a way to prove that the absolute minimum of the viscosity can be expressed just in terms of three fundamental constants [ Science Adv 6 (2020), April issue ]. Their amazingly simple reasoning, based on dimensional analysis and limiting arguments, is that around the minimum the path length L should be of the order of the Bohr radius, L~aB, with the density r = m/aB3; the molecular velocity to move a distance ~aB is estimated as w~aB/tD=wDaB/2p, with wD the Debye frequency. From which the static viscosity at the minimum is obtained as h = mwD/(2paB), and the kinematic viscosity as n =wDaB2/2p. Then, their further step is a little more than a back of the envelope calculation (their derivation is slightly more refined that this, but not much more), namely they take the ratio of the average phonon frequency hwD, to the typical molecular energy scale, the Rydberg energy ER, to obtain hwD/ER = (me/m)1/2. Substituting this expression for wD in the equations above, the viscosity at the minimum is obtained as n = h/4p(mem)–1/2. Finally, by entering the minimum molecular mass, that is the proton mass mp, the absolute minimum of the viscosity is nmin = h/4p(memp)–1/2 ~ 10-7 m2/s, in amazing agreement with experimental data. I am absolutely fond of this way of doing physics, fiddling with dimensional analysis and simple analogies, trying to apply fundamental physics concepts to some remote phenomenon, and ending up improving the understanding of the fundamental concepts (even if, in many cases, we could not throw much light on the remote phenomenon itself).
It may be interesting to note that the minimum dynamic viscosity so obtained is a function of h–5, in fact hmin= nmin r ∝ nmin/aB3 ∝ h / h6 . This means that the value at the minimum must be very sensitive to small variations in the Planck’s constant, a problem related to the “coincidences” invoked to justify the so-called Anthropic Principle. It is speculated that since the viscosity of water at ambient temperature is already close to the minimum, living cells should have adapted to a very different viscosity, if the constant h were just a little smaller or larger than its current value; probably the whole metabolism and biochemical kinetics would be largely different from what we know.
Not content with their viscous findings, our two scientists (now joined by Bartomeu Monserrat and Chris Pickard, of Cambridge) applied the same “ingenuity” and dimensional arguments to the problem of the maximum speed of sound, us, which they succeeded in writing down, again, as a function of just a few fundamental constants: umax/c=a(me/2mp)1/2, with a the fine structure constant and c the speed of light. The limiting value they obtain is 36,000 m/s, about twice the maximum value ever measured on Earth, for perfect diamond samples. Again, the agreement of their predictions with experimental data is very good, for elemental solids, considering that the speed of sound is dependent on many factors, such as type of bonding (ionic, covalent, metallic…) and crystal structure. They also attempt at providing a prediction for molecular hydrogen under high pressure, by comparing with the results of DFT simulations. This prediction is challenged by previous estimates, according to which the maximum sound speed should be equal to c/31/2, but such are the (usually) weird results from string theorists. A more reliable limit is deduced by astrophysicists studying the hyperdense nuclear matter of neutron stars (that, by the way, also contain fully degenerate protons and electrons), in which the extreme pressure, reaching more than 1020 times that at the center of the Sun, can bring the sound speed very close to c. [ see e.g. Phys Rev Lett 114, 031103 (2015) ].
However, the “universal” limit to the speed of sound for ordinary matter could be even more interesting than the viscosity one, since us enters in several other quantities of solid-state physics. For example, it appears at the denominator of the specific entropy and specific heat of solids, meaning that the absolute upper limit for us sets an absolute lower limit for both s and cV.
Moreover, you attentive readers will have noticed that the formula above for the dynamical viscosity looks dangerously similar to the empirical equation for the thermal conductivity, K=cVwL/3, with the density replaced by the constant-volume specific heat, and the molecular velocity and mean free path replaced by the corresponding “phonon” quantities. I bet that Kostja and Vadim could be already preparing for us some other fundamental surprise, maybe this time concerning the thermal properties…
Have a good Sunday, and a very very Merry Christmas to everybody!
