We are in the great city of Prague, November 23, 1911. The young Albert Einstein has just accepted his first assignment as full professor of theoretical physics at the Karl-Ferdinand German university of the Bohemian capital. The hard days are over, and this period of relative relax pushed him to fiercely work at the missing pieces his theory of general relativity, plus a number of other minor subjects, among which two papers with Ludwig Hopf on the interaction of a material oscillator (a “molecule”) with electromagnetic radiation. In these and other works of the period, Einstein is still trying to recover atomistic properties without making recourse to the quantization of the energy, a rehabilitation program which he shared with Planck: both being the main culprits for introducing the concept of quanta, both desperately trying to reject the truth as an abomination. Let us then imagine Einstein sitting at his desk, when suddenly an article from a magazine comes up before his eyes. He startles. That piece is about Marie Curie Skłodowska, and is not about her successes which brought her the Nobel Prize in Physics in 1903, the first woman to receive the prestigious recognition, but about the scandal that represents her private life.
For some time by then, the 45-years old Marie has been in a relationship with the slightly younger Paul Langevin, recently separated from his wife. Their story becomes public, sparking indignation among academia, and gossip weighs on the already sad story of Marie. Three years after receiving the Nobel together with her husband Pierre, Marie is widowed in a tragic accident: on a rainy Parisian night, Pierre slips under a horse-drawn cart and dies instantly. In 1910, however, four years after her loss, she starts getting closer to Paul, a former student of her husband. The two fall in love and start dating. Despite being separated from his wife, Langevin is still technically married and his relationship with Marie arouses the ire of his ex-wife, who does not accept the separation, now pointing at Marie as the only responsible for the end of their marriage. And she decides to take revenge: she orders a trusted man to sneak into the apartment where the two met, and steal their love letters. Not even time to read them in full, m.me Langevin immediately diffuses them to the press: the scandal is served. And the newspapers of the time, not much different from those of our current times, do not go light on the story: they swell the facts, sifting through Marie’s life, even portraying her as the “perfidious foreign Jew (which by the way she was not) guilty of destroying a happy family”. It takes very little to forget all the woman’s successes, leaving only and exclusively her “scandalous” reputation as a family wrecker.
In October, Marie participated to the first Solvay Conference in Brussels, where she met Einstein, who was immediately struck by her “brilliant intelligence”, defining her a “modest and honest” woman (enclosed photo: Marie is seated, talking to Poincaré, behind her on the right Einstein seems to be arguing with Langevin). Upon returning to Paris, Marie found an angry crowd waiting at the front door, forcing her to take refuge with her daughters at a friend’s house. Meanwhile Einstein returns to Prague, where he learns of the scandal. Maybe sympathetic because his own relationship with Mileva Maric was turning increasingly bitter, he reacts furious and indignant at the cruelty of the press that had made a private situation public, with the deliberate intention of destroying Curie’s scientific reputation. As a matter of fact, the French Academie had refused in January her application to join the Les Immortels, only to be publicly scorned by another Academy in Stockholm, which the same year 1911 would award Marie Curie a second Nobel, this time in chemistry, one of the only four persons ever to have received this honor. That night of November 1911, Einstein puts aside his precious work and hastily writes the following letter, which is often reported in essays and books about Einstein’s life and legacy:
Highly esteemed Mrs. Curie,
Do not laugh at me for writing you without having anything sensible to say. But I am so enraged by the vulgar manner in which the public is presently daring to concern itself with you that I absolutely must give way to this feeling. However, I am convinced that you consistently despise this rabble, whether it obsequiously lavishes respect on you or whether it attempts to satiate its lust for sensationalism! I am impelled to tell you how much I have come to admire your intellect, your drive, and your honesty, and that I consider myself lucky to have made your personal acquaintance in Brussels. Anyone who does not number among these reptiles is certainly happy, now as before, that we have such personages among us as you, and Langevin too, real people with whom one feels privileged to be in contact. If the rabble continues to occupy itself with you, then simply don’t read that hogwash, but rather leave it to the reptile for whom it has been fabricated.
With most amicable regards to you, Langevin, and Perrin, yours very truly,
A. Einstein
P.S. I have determined the statistical law of motion of the diatomic molecule in Planck’s radiation field by means of a comical witticism, naturally under the constraint that the structure’s motion follows the laws of standard mechanics. My hope that this law is valid in reality is very small, though.
And here stops my interest for the unfortunate love story of Marie and Paul, because my attention is now caught by that “PS”. After so much display of sentiment and human feelings, Einstein can’t hold himself from adding a spare science note. What is the “comical witticism” that should make a diatomic molecule in the year 1911, to follow the laws of standard (not quantum!) mechanics?
That same day, Einstein had written another letter to H. A. Lorentz, in which he begs forgiveness for not accepting the invitation to go to Utrecht, while recommending Peter Debye in exchange. And then he starts discussing his attempts to get rid of quantization (which he calls “the h-disease”, or “h-Krankheit”) while applying classical mechanics and the Maxwell-Boltzmann distribution to at least three different radiation problems, always falling back on the Rayleigh-Jeans energy-divergent formula. This explains a little better what he intended by “comical witticism”, and sheds light on the work he was conducting in parallel, trying to understand the specific heat of molecular gases.
The contribution of rotational motion to the specific heat of molecular gases had been a puzzling subject since the whole second half of the XIX century, and many were trying to apply the new quantum formulas to solve this problem. Cracking the rigid rotator problem should have been a simple matter since the theory has only one adjustable parameter, the moment of inertia. But no satisfactory theoretical description of the specific heat of hydrogen at low temperature had emerged with the classical treatment, and with the (old) quantum theory alike. No wonder that this was one of the most debated themes treated at the 1911 Solvay conference.
The first hint at a possible solution came from the Nernst experimental measurements and his theorem, which indeed had nothing to do with quantum theory per se, but led to the conclusion that the specific heats of any substance should go to zero approaching the absolute zero. In 1912 Arnold Eucken, one of Nernst’s students, succeeded in packing 0,2 moles of H2 in a 39 cm3 steel chamber (that is, a pressure of more than 100 atm), and was able to measure the specific heat down to about 30 K, finding that the points indeed converged towards zero in a kind of sigmoidal function. At the 1911 Solvay Conference, Nernst talked mostly about solids and said little about gases; he presented just a sketch of theory with rotators exchanging harmonic oscillator quanta with Planck resonators. Lorentz suggested to apply the quantization also to the energy of the rotator, but others like Langevin and Lindemann replied that it would not make sense to quantize the rotational motion, which “had to be” continuous.
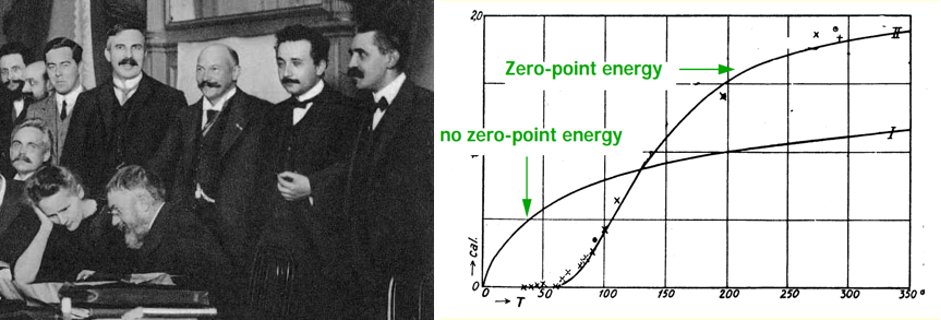
By 1910, Einstein had found an equation for the specific heat of diatomic molecules based on Planck’s formula, but as he wrote in a letter to L. Hopf, the matter was “problematic”. Already Planck in his papers on the “second quantum theory” (1910-11), in which he was trying to restore a continuous energy, admitting only jumps across finite phase-space cells, had found an extra energy term of hv/2 for each oscillator. This extra term was independent on the temperature and had no effect on the overall blackbody distribution. Einstein and Otto Stern, in their 1913 paper (Einige Argumente für die Annahme einer molekularen Agitation beim absoluten Nullpunkt, Ann. Phys. 40 (1913) 551) used the Planck distribution for the continuous energy of the rotator: E=hv (1/exp(hv/kT)–1 +1/2) and included the zero-point energy, but still without assuming the quantization of energy. The zero-point contribution is mathematically necessary, for the partition function of the solid to take the well known sinh–1(E/kT) form, which leads to Einstein’s specific heat formula of 1907. But how about the gas? To their greatest surprise, the predicted curve by Einstein and Stern was in excellent agreement with the only low-temperature cv data available at the time, the experiments by Eucken; the figure 2 in their paper (included here) clearly shows that inclusion of the zero-point energy is necessary in order to obtain the agreement, while excluding it leads to a completely different temperature dependence of cv.
Besides using a continuous (not quantized) energy, a major flaw in the Einstein-Stern paper was the assumption – similar to his theory of the ideal solid – that all molecules have the same rotational frequency; moreover, in the second part of the paper their zero-point energy turned out to be hv, twice the Planck’s value. Einstein was aware of the untenability of the model, something that in his view however depended chiefly on the inconsistency of the notion of zero-point motion, which he found absurd, also leading to apparent incompatibilities with superconductivity. The paper met with great success, but at the second Solvay conference of 1913 Einstein no longer believed it, and affirmed that zero-point motion was dead as a doornail (mausetot ist). By that time, he was busy with the final details of the general relativity, tightly working with Marcel Grossman, and he practically abandoned the problem.
After 1913, a succession of theorists starting with Ehrenfest applied quantized rotator models to obtain he specific heat of hydrogen, at first with only one degree of freedom, and then with several degrees of freedom. None succeeded in getting better agreement with Eucken’s data, than the wrong model of Einstein and Stern did. The solution of the puzzle had to wait another 10 years, when Heisenberg for the first time introduced in the new version of quantum mechanics that was developing, the notion of indistinguishable particles. Friedrich Hund applied this idea to the calculation of molecular spectra, with some apparent success. However, another part of the problem was in the measurements of Eucken, which were no longer precise enough for the degree of refinement that the modern theory was approaching. New experiments on the spectrum of molecular hydrogen in the far ultraviolet after 1925 led to independent measurement of the moment of inertia of the H2 molecule. It was up to David Dennison, who had worked one year with Schrödinger in Zurich, to put together the pieces for the final solution. He identified the requirement that the square modulus of the wave function must be single-valued, therefore finding two separate solutions (which later were attributed to ortho- and parahydrogen) for the specific heat, of which he believed only one could correspond to the reality. After a visit to Fowler in Cambridge, he read the recent papers by Heisenberg on the nuclear spin, whose account allows to mix even and odd states, and could eventually arrive at the final conclusion, that the measured specific heat at any temperature is a mixture in different proportions of the two states.
A seemingly simple problem contained all the germs of the new quantum theory. But Einstein was already sailing towards other shores, his bow set on the stars. The zero-point energy, which he so vigorously rejected, today has found unexpected links with his cosmological constant Lambda, which he also defined “my greatest blunder”. So, the product of two errors makes for one right?
