Imagine waking up in a Salvador Dalí painting. You reach over to touch your alarm clock, only to discover that it melted into a puddle during the night. The sun rising outside your window illuminates the hedge in your garden now up in the sky, lurking a hundred feet tall over its stretched stems. In this confusing reality, everything is slowly but continuously distorting itself. Your coffee mug morphs into a doughnut, and the sugar-glazed doughnuts stretch up into thin cylinders, as if they are made of putty that’s been pinched and pulled. You start to read the daily news, and subtly you realise letters like L, M, C, Z, N, sliding into each other and becoming indistinguishable. Everyday things seems to lose their identities, and shapes seamlessly are turning into one another. That is the world of topology.
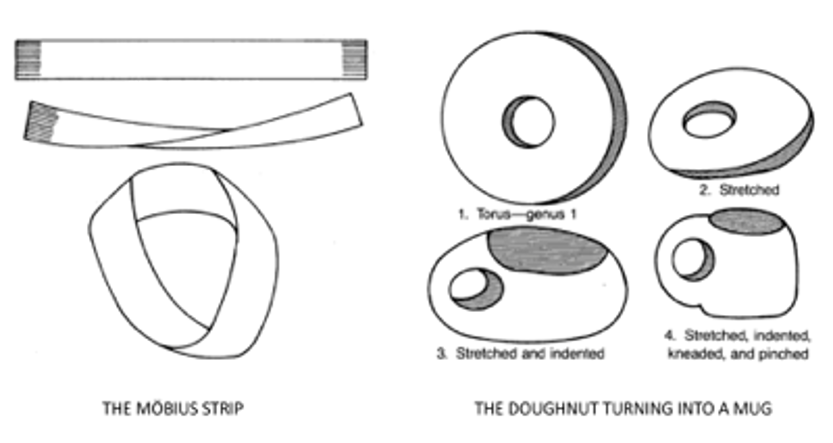
The story of topology begins almost 300 years ago, when Leonhard Euler heard about the following puzzle: could a traveler stroll through the city of Königsberg, and cross each of its seven bridges exactly once? Trying to solve the problem (which he initially dubbed as “banal”), he took an unusual approach. Euler believed the problem to concern geometry, but not the geometry well known by his contemporaries, involving measurements and calculations, but instead a new kind of geometry, which another great fellow mathematician, Wilhelm Leibniz, referred to as Geometria situs (“geometry of position”). Hence, Euler ignored the details of the city map. Forget about the lengths of the bridges and distances between them. Ignore the size of the city’s central island. Build a mental model of the city, distort it however you like, stretch, pinch, but never break, and the problem does not change. All that matters, Euler said, was the number of bridges and the number of landmasses they connected. Simply by counting these, he showed that the problem was unsolvable. This way of reasoning was the initial seed of the new branch of mathematics dealing with intrinsic properties of shapes. Topology describes properties of objects that do not change during continuous deformations. For example, an object known as Möbius strip (see enclosed figure, left) will always have one continuous edge and one continuous surface, no matter how much it is stretched or twisted. Similarly, a mug and a doughnut are topologically the same object, since they are defined by the existence of a single hole (see figure, right). Topology is also what properly differentiates a line from a surface and, more broadly, what constitutes a dimension. However, for the three centuries that followed the “Königsberg defeat”, topology was not applied in a serious way to any serious important problems. Then, in the 21st century it started to became a force to be reckoned.
In February-March 2009 I was spending a couple of months in Tokyo, collaborating with people at the IIS in the University of Tokyo. That was already my third short term in Japan. Living in Japan as a non-Japanese can be a rather pleasurable routine, as it offers the ingenuous traveler almost every day a plentiful occasions of new experiences and serendipitous discoveries. I documented my second and third travels in a blog page (jerryinjapan.blogspot.com), then I lost interest in the novelties and stopped writing. One cloudy and rainy February afternoon I was on the Tsukuba Express riding back to my micro apartment in Shibuya, after a 3-day symposium held at the Center for Materials Nanostructures (MANA). An old European guy with white hair and unkempt beard sitting next to me was on the chatty mood, and we started talking about this and that. Then I recognised him.
“Hold on… you are Heinrich Rohrer, the Nobel Prize winner”, I said.
“Yeah, that’s me – he replied – but don’t say it too loud.”
Heinrich had just given an opening talk at the Tsukuba symposium about surface probe microscopy and nano materials. I told him I had greatly enjoyed his lecture. He said he was tired of being invited all over the world to deliver always the same lecture. “I would like to speak about something more recent and more interesting – he almost whined – but each time they want me to repeat the talk about the history of the STM invention. It’s been always like that, since I got that damned prize.” He looked indeed quite tired and weary, maybe it was the rainy evening, maybe it was his old age that started to claim its toll. We kept discussing about more mundane cases, for example I remember him saying that post-docs should never be allowed to continue in the field where they made their Ph.D., something which I quite wholly endorse. Then we arrived in Akihabara, where the train stopped, and we both had to change to different lines. I said hello and good luck to him, and a final question:
“What is going to be the next hot area in nanotechnology, according to you?”
He answered: “I think topological materials, that’s very likely.”
At that time, in 2009, the very first topological insulators based on Bi-Sb had just been identified experimentally. My bet would have been instead on high-Tc superconductivity, since (shame on me) I had never heard a word about topological materials.
In the ten years or so that followed, topological materials exploded, they have been understood in great depth, and experiments have accumulated. In the most naive description, these are materials in which bulk properties determine a special, and physically different behaviour along the surface or an edge of the crystal. For example, a bulk insulator becomes a conductor at some of its surfaces. Theory has been paramount in guiding experiments, and even exotic entities such as magnetic monopoles and Majorana particles, once exclusive hunting reserve of particle physicists, have turned into subjects of solid-state topological studies. One interesting thing about these materials, besides the fact that they have been predicted theoretically well before being discovered, is that the concept of invariance under topological transformation is a very general, mathematical notion. The idea can therefore be extended to different physical systems, beyond the domain of solid state physics where the concept has been initially demonstrated. A first area into which topological invariance has been extended is that of photonic materials. Suitably designed electromagnetic media (metamaterials) can behave as photonic analogues of a topological insulator. So-called non-trivial photonic states, similar to those that have been identified for condensed-matter topological insulators, seem to exhibit spin-polarized one-way propagation of photons, and are robust against disorder. In this way, one-way photon transport could be attained without application of external magnetic fields, or breaking time-reversal symmetry (see e.g.: Khanikaev et al., Photonic Topological Insulators, https://doi.org/10.1038/nmat3520 ).
Both in solid state and photonics materials, the key to topological effects seems to be the underlying regular lattice, whose peculiar periodicity can determine the required properties. The situation changed in 2017, when a team based at Brown University (Brad Marston) and ENS Lyon (Pierre Delplace and Antoine Venaille) started studying generic models of fluids from a topological perspective. The three scientists were interested in some unusual waves in the atmosphere and oceans at the equator, known as Kelvin and Yanai modes. Such modes can be described as classical solutions to the wave equation, but they are confined to the Earth’s equator; they are persistent; and they only travel eastwards, never westwards. They noticed that these equatorial waves had topological characteristics. First of all, the slim layers of the Earth’s atmosphere and oceans can be approximated as 2D. Second, the constituent air and water molecules are, like electrons in the quantum Hall effect, pushed into a circular motion by the Coriolis force acting perpendicularly (and breaking time-reversal symmetry, just like the magnetic field in the solid-state case). Without having to solve any classical wave equations with ungainly polynomials, they proved that the equator should harbour two unidirectional equatorial waves. Both these waves are known to influence the El Niño Southern Oscillation in the Earth’s ocean–atmosphere system, which in turn has a significant climate impact, causing incidents of drought or flooding in equatorial countries. (see Topological origin of equatorial waves, https://doi.org/10.1126/science.aan8819 )
More or less at the same time, apparently Inspired by a talk by Marston, Cristina Marchetti and her coworkers at Syracuse University, New York, started exploring topology in a very different type of fluid system: active matter. Such matter consists of any collection of units that dissipate energy to perform work and generate motion, leading to sustained and local breaking of detailed balance. Examples abound in the living world, ranging from bird flocks, to bacterial suspensions and migrating cells, and include synthetic analogues, such as vibrated granular media and self-propelled colloids. Like the Earth’s atmosphere and surface, these system often have a curvature. Collective cellular motion on curved surfaces is ubiquitous in developmental processes, such as morphogenesis and embryonic development, or when cells migrate in the gut, or on the surface of the growing cornea, and it also affects cell division. The difference with the Earth’s atmosphere and surface, is that biological active matter is not subject to a perpendicular external force such as the Coriolis force. But the fact that the matter is active and propels itself breaks time-reversal symmetry. Marchetti’s first paper (see Topological Sound and Flocking on Curved Surfaces, https://doi.org/10.1103/PhysRevX.7.031039 ) is already highly cited, and has instigated a number of other groups to work along these lines. In several examples, active systems exhibit spontaneous flows induced by self-propulsion of microscopic constituents, and can reach a non-equilibrium steady state without an external drive. In analogy with the quantum anomalous Hall insulators, active matter with spontaneous flow appears to display topologically protected sound modes (see e.g.: Sone & Ashida, Anomalous Topological Active Matter, https://doi.org/10.1103/PhysRevLett.123.205502 ). These long-wavelength propagating sound modes get a gap in their band structure just by the curvature of the underlying substrate, and are localised at particular geodesics on the curved surface, such as the equator of a sphere. Clearly, biology is too complex to speculate about such effects for any real-life particular systems. However, some types of active matter are already known to host waves. For instance, cells involved in wound healing are known to transmit stress waves, which may be involved in guiding the tissue’s growth and maintaining its integrity until the wound is fully healed. Given that wounds often occur on curved parts of the body, it is not inconceivable that in some situations these waves could also have a topological character ?
Another exciting area of this new lattice-less fluid topology is plasma physics. The same Brad Marston has now moved to collaborate with scientists in this field, and in a first theoretical work on plasma magnetically confined in an ideal cylindrical geometry, they already identified a surface wave of electrons, which they christened “gaseous plasmon polariton”, that should manifest on the outer surface of the structure. Then, by collaborating with people in Los Alamos, they moved to the tokamak, the doughnut shaped geometry used by nuclear fusion reactor studies. The tokamak longitudinal cross section is not circular, like in a Dunkin’ Donuts doughnut, but has the shape of a “D” formed by the strong magnetic field that maintains the plasma. Marston, Jeff Parker and coworkers predicted that the curved regions in the “D” where the magnetic field changes from positive to negative should harbour topological waves (see: Nontrivial topology in the continuous spectrum of a magnetized plasma, https://doi.org/10.1103/PhysRevResearch.2.033425 ). Plasma physicists have always known about the existence of such boundary waves, that they call “reverse shear Alfvén eigenmodes”, as a major source of problems in disrupting the plasma-matter equilibrium within the fusion reactor. The discovery that such Alfvén waves could coincide with topological waves does not change the physics of the problem. As in the case of equatorial waves in the Earth’s atmosphere and active matter systems, however, the result provides the tantalizing prospect of more topological insights into tokamaks, which can currently only confine plasmas from minutes to hours before they die out. Might it be possible that one could find the tokamak conditions that deliver a “topologically protected” state of fusion – in other words, one that can be sustained indefinitely and give us the nuclear fusion reactor of our dreams?
The physics of topological fluids is just starting, in such diverse field ranging from geophysics to active biological matter to plasmas, and it could promise exciting new results.
