Two weeks ago, we left Phil Anderson mumbling about massless bosons, on his way back from Cambridge in the summer 1962. He would end up writing a short paper, about one year later, in which he added the word “plasmons” plus an interesting “,” to Schwinger’s title (Plasmons, Gauge invariance, and Mass). To understand – as much as possible, and sorry for my limited capabilities – the issue, we must include some further notions about gauge invariance and the BCS theory of superconductivity.
Gauge invariance is that peculiar mathematical relation for which, by adding the gradient of a scalar field to a vector field, nothing changes in the physics. As I already noticed in a previous letter, this is due to the fact that the field we are looking at, for example the classical electromagnetic field, is overdetermined. The two vectors E and B have six components, but the 4-potential (φ,A) has only four: the two undetermined components are the gauge freedom, which imply a symmetry of the electromagnetic field. For example, one can choose arbitrarily the zero of the electric potential V, which allows birds to sit on one conductor (but only one of the two) of high-power transmission cables without burning into ashes. (En passant, I note that a similar indetermination holds also for the matter elastic field: the stress tensor in classical mechanics is also gauge invariant, and liable to adding a zero-divergence quantity without changing the final results.) The important point is just that gauge invariance reveals an underlying symmetry, and this (Noether’s theorem) implies a conserved quantity (e.g., charge). For example, the quantized Lagrangian of the electromagnetic field in QED would lose gauge invariance if a term proportional to m2A2 is added, hence m=0 constrains the photon to have no mass.
Now, the original BCS theory of superconductivity had a problem with gauge invariance. As we know, in this theory paired-electron states can have an energy less than the Fermi energy and, if the temperature is low enough so that thermal energy is negligible, bound states (“Cooper pairs”) of two electrons can form, with a non-zero energy also at p=0. This is a breaking of the symmetry of the free electron gas, and the non-zero energy is the so-called “superconducting gap” energy Δ. However, to produce correct results the original BCS theory had to be corrected (details omitted!) in a way that, unfortunately, made also a lot of different excitations to appear, aside of the paired electrons. In particular, Goldstone bosons called “phase modes”, a kind of collective phonon-like modes, would fill the gap with lots of extra energy levels. Anderson already had made a point in a 1962 paper, showing that in the real superconducting system in which all the interactions are included, such modes cannot exist and the gap is clean. So, when he heard about the Goldstone-bosons problem in high-energy physics, he was completely prepared for the battle.
In the BCS theory, the “gap” energy appears in the energy spectrum of states, as
e’k=[(ek–μ)2+Δ2]1/2.
Note that, in the absence of Δ, the relation between e’k and ek would be linear, and give the Dirac cone. But now, if you remember Einstein’s relativistic energy-momentum relationship,
E=[c2p2+(mc2)2]1/2,
this would be similarly linear if the electron mass were zero, and thus E=cp (massless fermions give Dirac cones). Therefore, the “gap” energy Δ of the superconducting state actually looks like a kind of mc2 mass term, just derived from the pairing interaction of the electrons. This point had been noticed by Yoichiro Nambu, who in 1960 had suggested to use a BCS-like model to generate mass for the massless fermions of the standard model (which, by that time, was not yet “standard”), just from their interactions. This eventually turned into the Nambu-Jona Lasinio model, in which most of the nucleon masses arise from their interactions, and not just from summing up the quark masses. But also in this case, Goldstone massless bosons appeared from nowhere, problematic, since without these (never observed) bosons the theory would break both charge and baryon number conservation.
In his 1963 paper, Anderson used as an analogy the plasmon theory of the free-electron gas, as a realistic example satisfying Schwinger’s suggestion that the requirements of gauge invariance and particle conservation do not imply massless bosons, if the (symmetry-breaking) interaction is strong enough. He did not even bother with quantum mechanics and relativity, but focused just on the classical non-relativistic model of plasmon. He could show that the dispersion relation for plasmons is quadratic in the wavevector, just like in the above BCS superconductor, as if the plasmon had an effective mass. He interpreted this as the effect of symmetry breaking in both systems, which creates from nothing the Goldstone scalar-boson excitations. Then the vector (spin-1) gauge field (the photon) and the scalar (spin-0) Goldstone boson created by the broken symmetry (long-range charge oscillations for the plasmons vs. “phase modes” in the Cooper pairs), both massless, combine in the interaction, and result in the observable, massive vector bosons (effective-mass plasmons vs. a “massive” photon as in the early London’s theory). In a more picturesque description, the Goldstone boson is “eaten” by the gauge field boson, to become its third, longitudinal component (remember that both the classical electromagnetic wave, and the quantum massless photon, only carry the transverse components of E and B), thereby giving it a mass. This is what is today called the “Higgs mechanism”… which was however first described by Anderson! Spread the Gospel According to Anderson, so to say, and also for the model of electro-weak interactions by Glashow, Salam and Weinberg, again plagued by the flood of invisible massless bosons, this will be the solution leading to the discovery of the three massive vector bosons Z0, W+ and W–, which would lead the trio to the 1979 Nobel prize, followed by Rubbia & Van der Meer in 1984, and T’Hooft & Veltman in 1999, who proved the theory to be renormalizable. And, of course, the Nobel prize of 2013 to Higgs and Englert. One idea, four Nobels.
If you are a little lost by now, just remember the following: (1) gauge invariance of a field implies a symmetry and some conservation law; (2) the spontaneous breaking of such a symmetry makes massless spin-0 (=scalar) bosons (Goldstone modes) to appear; (3) the massless spin-1 (=vector) boson of the broken-symmetry field, can acquire a mass by canceling out the Goldstone. Important note: the fact that the vector boson carrying forces (e.g. the photon) acquires mass, makes the long-range (e.g. Coulomb) force to become short-ranged.
Peter Higgs also took up the magic idea of Anderson in 1964, and recast it in a relativistic model in two papers, the second one being the key (the PRL Broken Symmetries and the Masses of Gauge Bosons). To be fair, several other theorists, R. Brout and F. Englert, and the trio G. Guralnik, R. Hagen, T. Kibble, had published a PRL paper along similar lines that very same year. Definitely, the idea was in the air. However, Brout and Englert did not mention at all Anderson’s work, while the GHK paper cites Anderson just for a less important 1958 paper. Higgs, instead, gives full credit to Anderson’s 1963 paper, by writing in the introduction: “This phenomenon is just the relativistic analog of the plasmon phenomenon to which Anderson has drawn attention.” If you think that Anderson would have deserved 1/3 of the prize (of which he got 1/3 already in 1977) you are probably right. Strangely, the Nobel committee (somebody say, maliciously, just to keep Anderson out of the business) used the argument that Higgs “properly” made the theory relativistic, while Anderson had shown that the (ahem…) Higgs mechanism is in fact independent of relativity, and even of quantum mechanics.
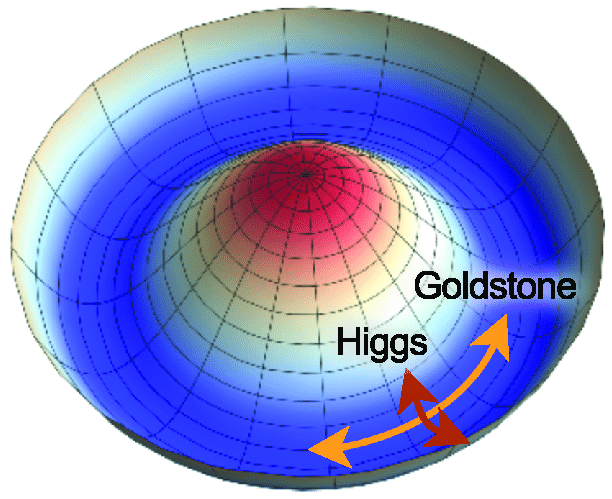
What was then, the important addition that Higgs (and Brout and Englert) made to this beautiful piece of theory? The Anderson model had no need to introduce an extra particle to create the plasmon mass or the superconducting instability, it was just needed to fully include the interactions to get it. As Anderson himself commented, “Higgs and his friends were punctilious about having the mechanism explicit”. To make the symmetry breaking explicit (remember my previous example of the pushed rod that bends) they went back to Goldstone et al., and studied the case of a complex scalar field Φ=(Φ1+i Φ2) interacting with the electromagnetic field. This is the famous “Mexican hat”. I spare you many details (if somebody is interested, I can send you a simple two-page calculation that makes all clear), and let’s go directly to the conclusion: in this case two scalar bosons appear in the theory, one (Φ2) is the traditional massless Goldstone, and the other one (Φ1) is a massive scalar boson, that will later get known as the “Higgs’ particle”. This is obvious by looking at the Mexican hat potential (see enclosed figure). When a finite value to Φ1 is given (the non-zero vacuum expectation value of the ubiquitous Higgs’ field) the initial symmetry is broken, and the “valley” is now populated by two orthogonal excitations: the Φ2 running around the valley has a flat slope and is therefore massless, instead the Φ1 across the valley is a kind of harmonic potential, and therefore has a mass. This is the Higgs’ boson associated with the symmetry-breaking interaction.
The final touch came from Samuel Weinberg, with his 1967 PRL (A Model of Leptons), a little masterpiece of a paper in which he proposed the first block of the unified electroweak theory of weak nuclear forces and electromagnetism. He incorporated the Higgs mechanism of cancellation of massless bosons, to provide a finite mass to the electron (while fixing the neutrino mass to zero), and introduced a Higgs field that undergoes spontaneous symmetry breaking, resulting in the generation of masses for the weak gauge bosons (W+, W–, and Z0) while the photon remains massless. Wow. In the following years many others used a similar approach to provide masses for all the fermions, by making the Higgs’ field to interact with the quark fields via Yukawa (finite-range) coupling, an area that is still under very active research.
Some say that the mass of the Higgs’ boson, despite the very good coincidence between the predicted and measured values, is way too small to fix the quark masses in a stable way at high energies. And some other say that the Higgs’ field becomes “trivial” and negligible at higher energies. Yet some others, say that the mass originated from Higgs’ field is just a minor part of the mass of the universe, which is mostly made of dark matter, and maybe we should look for something else and put Higgs to the trash bin. Higgs’ remarkable second paper of 1964 contains a mere 660 words, 4 equations and 9 references. That’s all it took to get a Nobel, and make one of the most troubling discoveries of physics.
