Like almost any Italian student of physics of the 70s, I did my share of the experimental measurement of the half-life of the muon. Although I followed the theoretical physics curriculum, we had to pass one painful exam each year in experimental physics. In the beginning, I admit, it was even fun; but for the 4th year there was the big barrier of practical electronics first, and the muon experiment in the second semester. The muon half-life experiment in Italy is a long-standing tradition, dating back to the Panisperna group and the first measurements by Franco Rasetti in 1941, with the delayed coincidence method (which we students were desperately trying to reproduce, see below), down to the famous “CPP” (Conversi-Pancini-Piccioni) experiment of 1945 that everybody in our small world thought of as yet-another-failed Nobel prize.
The story of the meson is the story of a long chase. In 1935, Hideki Yukawa came out with his theory of short-range forces being mediated by vector particles, and estimated that, given the radius of the nuclear force of about R~2-3 fm, the mass of the strong force vector particle should have been around 200 times the mass of the electron (that is a simple calculation: start from 𝛥E𝛥t~mc2·(R/c)~ℏ, and you get m~100 MeV). Two years later, Anderson and Nedermeyer identified a highly penetrating charged particle in the cosmic rays, with mass in the range of 200-240 electron masses, which they called “mesotron”. In 1938, Heisenberg explained that the measured lifetime of such a fast particle would display the relativistic time dilation.
In 1941, Rasetti built his ingenious delayed-coincidence apparatus, and obtained the first independent estimate of the muon lifetime, at 1.5±0.3 microseconds. His idea was to measure the intensity in three inline detectors with well-defined time windows, one at 15, one at 1.95, and the third at 0.95 𝜇sec; the differences N15–N1.95 and N15–N0.95 give the number of muons not yet decayed between the two windows, and allow to estimate the lifetime from an exponential decay law (however, he used Geiger detectors to count the coincidences, and the intrinsic dead-time of the Geigers led him to such a too low value; in the modern university version, we students used blocks of plastic scintillator). That same year, Bruno Rossi (emigrated in the US because of Italian anti-Jewish laws) did his famous experiment that confirmed Heisenberg explanation, and represented the first true verification of relativistic time dilation, obtaining a lifetime of 2.15 𝜇sec; this result however would remain unknown to his Italian friends until the end of the war. In the meantime, Marcello Conversi and Oreste Piccioni tried to improve Rasetti’s technique in the physics laboratory of Rome university. The tragic bombardment of Rome in June 1943, with more than 80 bombs falling on the university itself, forced them to move the experiment in the basement of Liceo (high school) Virgilio, near the Vatican City; they used a wooden chariot disguised as a grocery stand, pushed around the streets of Rome to carry the precious instruments. In October, Piccioni, who had tried to pass the front to reach the Allied army, was briefly arrested by the Wehrmacht in Frosinone, but got free a couple of weeks later, apparently thanks to a large sum of money paid by the father of another fellow prisoner. They continued working with other young students and supporting colleagues, like Lucio Mezzetti and Francesco Lepri (who was very skilled at finding RCA or Phillips tubes in the black market), to the underground experiment in the German-occupied Rome, risking every night to be arrested because of the curfew. Eventually, in March 1944, the experiment was up and running again, and they measured a much closer 2.3±0.15 𝜇sec. Their electronic circuitry was cheap and home-made, but extremely refined and precise. When Piccioni moved to the US right after the end of WWII, and saw the extraordinary development of electronics there, he felt at the same time ashamed by the comparison, and proud that they could reach such a precision with their manually assembled vacuum tubes.
After the success of the first experiment, by the end of the year Conversi and Piccioni started to build a variant of the experimental setup, with the help of Ettore Pancini (Ettore had some part in the early cosmic-ray experiments in the Alps, led by Gilberto Bernardini, but he had to leave for the army in 1941; after the armistice of ‘43 he entered the Resistance, became a commander of a partisan troop, and was a communist leader in Veneto until the end of the war). Now, according to Yukawa’s theory, the “mesotron” was strongly interacting with the atomic nuclei; therefore, positive mesons had a small capture probability because they are repelled by the nuclear charge, while negative mesons, attracted in the nucleus, should always have a large capture probability, and therefore a smaller decay rate. In the CPP experiment in Rome, two magnetic lenses allowed to select independently positive or negative muons: the striking result was that the ratio of positive/negative decays was about 25 with a large-Z absorber (iron), but close to 1 with a light-Z absorber (graphite). This was totally unexpected, and their paper [ in Phys. Rev. 71, 209 (1947)] greatly impressed, among others, Bohr (who called it “the Pinocchio effect”), Wick, Fermi, Weisskopf, Teller, who all started elaborating. Fermi in particular, who had received the news directly from Conversi prior to publication, calculated with Teller the relative absorption/decay rate, and declared that the muon could not be the meson of Yukawa, since it had no nuclear interaction with light nuclei (its interaction with heavier nuclei would be later explained by Bruno Pontecorvo). The actual mediator of the strong force was discovered in 1947, again in cosmic ray showers (the only source of high energy particles at that time, the first GeV machine would arrive only a few years later), and was the pion, with a mass of 139 MeV. Bethe and Marshak explained the process by which the pion disintegrates into a muon and a neutrino. Yukawa was right, and now we had two “mesons”: the one responsible for the strong interaction, and the muon that had nothing to do with the strong interaction.
But then, what the hell was the muon doing there? Why pions did not decay directly into electrons and neutrinos, but had to first go through this enigmatic particle? This was the great merit of the CPP experiment: the muon, an unwelcome guest, opened the way to a new family of elementary particles, the six leptons, which would become the most fundamental fermionic particles of the Standard Model, next to the six quarks. Luis Alvarez said, in his 1968 Nobel prize lecture: “As a personal opinion, I would suggest that modern particle physics started in the last days of WWII, when a group of young Italians, Conversi, Pancini and Piccioni, who were hiding from the German occupying forces, initiated their remarkable experiment.”
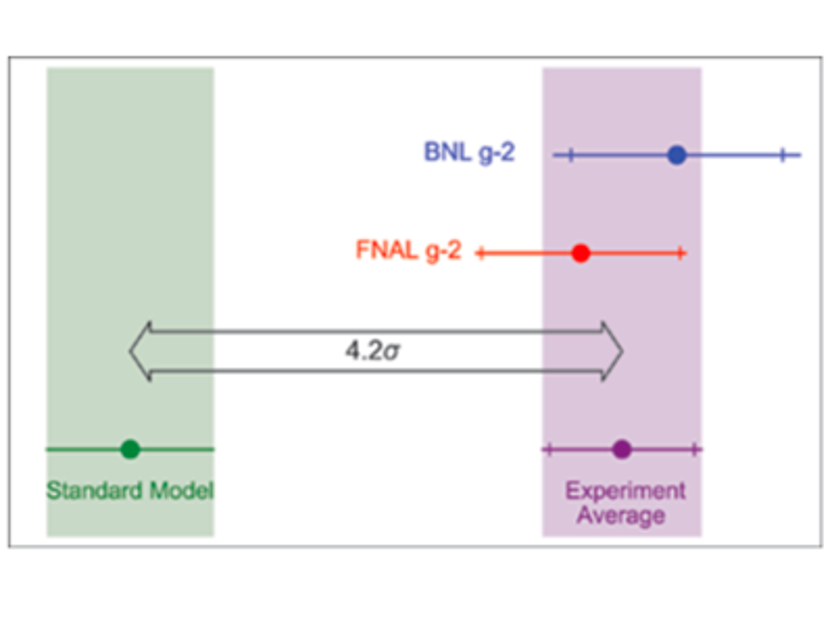
More than 75 years later, the quiet and humble muon comes again on the front stage, maybe to usher a new revolution in physics. Once again, it looks like physics understood “almost” everything, but some pieces of the puzzle are missing. And the muon is, once again, the strange piece which obstinately does not want to fit in. Today’s discovery links back to the “Muon g-2” experiment, started in Brookhaven more than twenty years ago, in which it was measured a value of the anomalous magnetic moment of the muon that disagreed by several parts per million with calculations based on the Standard Model. Physicists had long understood that our model of fundamental interactions, although very successful in many respects, is incomplete: the “Muon g−2” experiment provided a measurable discrepancy between a very precise quantum-mechanical calculation and an equally precise measurement of a fundamental constant. The magnetic moment of a particle is proportional to its spin and to its g-factor, which is exactly 2 for a point particle with half-integer spin as predicted by the Dirac equation. However, the muon is constantly interacting with virtual particles, photons, leptons, hadrons, the vector bosons and even the Higgs, which jump in and out of existence, with quantum-mechanical probabilities (the radiative corrections) calculable to a very high precision [see e.g.: Aoyama et al., Phys. Rep. 887, 1 (2020)]. This fluctuating cloud of particles modifies the g-factor. The amount by which it differs from 2 is characterized by the anomaly, a=(g−2)∕2, which is why the experiment is called Muon g−2. If the muon is placed in a magnetic field, its spin will precess about the field direction at a frequency that depends on the charge distribution of those virtual particles. Measuring the precession frequency provides a determination of the anomaly and thereby of the overall effect of the virtual particles.
Now, the next-generation “Muon g−2” experiment at Fermilab released its first results, confirming the mean value of the discrepancy, at a very convincing 4.2-sigma departure from the Standard Model (see figure). To comfort the Italian “muon tradition”, the paper published in this week’s Physical Review Letters, vol.126, 141801 (at the exceptional length of 11 printed pages, https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.126.141801 ) is co-authored by a large share of Italian scientists and institutions. As the Editor of PRL comments: “This mismatch could be the effect of new particles and new interactions that are considered by many natural SM extensions, such as supersymmetry, dark matter, and heavy neutrinos.” I admit I have a hard time at imagining “natural extensions” in the form of supersymmetry, dark matter etc., which seem anything but natural to me (at least at this time). Maybe we should start really looking for something new.
I do not remember whether our muon lifetime experiment in 4th year lab course actually gave the right result, but I presume we finally did it, since in our group we had two students who were very good at “that”. We had some good equipment that our lab teacher, professor Federico Palmonari, took on loan from the UA2 experiment at CERN where he worked. As a theorist, I was in charge with another student of the statistical data analysis (something that I always hated) but also wanted to do something more practical. My career as an experimentalist quickly ended the day I worked the preliminary scheme of a mysterious electronic circuit on a test breadboard, and forced an electrolytic condenser in the holes by inverting the polarity: the whole thing exploded with a huge bang, vigorously spreading the electrolyte all around and leaving myself scared, covered head to feet by a fine hairy powder. Since then I was unequivocally attached to the “Pauli effect”, and my only experimental occupation was to carefully wrap the blocks of plastic scintillator in black duct tape. For the final oral exam I had studied with great care all the material, and answered quite directly to all the various questions in electronics. Prof. Palmonari gave me a shameful note of 29/30, accompanied by the words: “I can see that you memorized very well your course, but I can also see that you don’t understand a word of the stuff you are talking about.”
