On January 14, 1995, a player at Bally’s Casino in Atlantic City bought $100 worth of Keno tickets (a popular lottery played on slot machines) with eight numbers selected on each ticket. After the draw, some mr. Reid Errol McNeal collected his receipts: one of those tickets had hit all eight numbers against odds of 230,000 to 1, which earned him a 100,000$ prize. Nobody looked more surprised than McNeal, suddenly attracting casino security controllers who had some serious questions before they would hand him his cash. Several aspects just didn’t look right. For example, mr. McNeal had no identification on him, and refused to take a cheque. But the loudest alarm bell was that no one had ever won so much at Keno, in the entire history of Atlantic City casinos!
State Troopers were called and asked to verify McNeal’s identity. When they got to his hotel room, things quickly began to unravel. In Errol’s room was a second gentleman, by the name of Ronald Harris, who immediately seemed odd and evasive to the investigators. He proved to be an employee of the Nevada Gaming Control Board, so something was definitely going on. But the question was: what? How does a Gaming Control Board employee predict the outcome of a bet with odds of 230,000 to 1?
The answer lay in mr. Harris’s day-to-day work as a computer technician. His job was to ensure that slot machine chips in Las Vegas were not interfered with, switched, or reprogrammed; the job required him to select different machines and check their EPROM chips. As a computer engineer, Harris had realised that computer programs had difficulty in generating long enough sequences of random numbers for the lottery games, and typically used algorithms based on past sequences to generate future outcomes. He figured that if the same program running on the same type of machine gave the same results, he could enter previous results of a target game, and use the same hardware (to which he had access) to make predictions. After officers came calling, Harris panicked and ran for the airport, leaving behind enough hardware pieces and papers to prove him guilty. On his return from Atlantic City, he was arrested and fired. You can test this little story yourself, by running a simple program on two different computers, and calling the random number generator (e.g., shuf in Linux, or jot in BSD-Unix) by feeding it the same initial seed on the two machines: the sequence of (pseudo) random numbers generated will be exactly the same.
In scientific computing, generation of large amounts of random numbers is a key requirement for many applications, the best known probably being the Monte Carlo method, which finds applications with many variants from statistical mechanics, to financial market analysis, to nuclear and radiation physics, and much more.
The general idea of Monte Carlo is: “Instead of performing long complex calculations, perform large number of simulated experiments using random number generation and see what happens”, nothing more than drawing strings of numbers in a slot machine (hence the namesake). Monte Carlo does not need to write down and solve equations analytically or numerically: it assumes that any system is described by probability density distributions of its variables. These probability density functions are sampled in a huge number of simulated experiments (the “histories”), each one of which reproduces one particular instance of the real system being simulated. Then, different properties of the system can be estimated by statistical averaging over the ensemble of histories. The key to adequately sample a probability distribution is just the availability of a very uniform (and truly random) random number generator.
And here comes one of the major problems: a Monte Carlo simulation requires to follow a very large number of “histories”, each of which has to randomly sample the many events occurring in the system. For example, if our intent is to study how a beam of cosmic protons travels through the thin atmosphere of Mars and is reflected off the surface rocks, we must follow each proton “history” by painstakingly accounting for all its interactions, changes of energy and momentum in each collision, and production of secondary particles in inelastic events. Each “history” may require hundreds or thousands of random numbers, and to obtain meaningful results we may need to follow hundreds of millions of simulated protons. Hence, the need to generate billions or trillions of random numbers, uncorrelated and evenly distributed, so as to have a good representation of the various probability distributions. In our recent study of proton and 𝛼-particle diffusion in the Martian atmosphere using the Monte Carlo code GEANT4 (F. DaPieve et al., Radiation Environment and Doses on Mars at Oxia Planum and Mawrth Vallis, JGR Planets 126, 1 (2021)] we generated not less than ~1010, or ~233 random numbers per run, a very typical figure in a Monte Carlo simulation.
An old legend circulating at the Argonne National Laboratory pretends that Enrico Fermi, while working at his analog neutron tracker (the FERMIAC, still on display in Los Alamos) produced by hand sequences of random numbers, by blind-eyed picking numbers from the pages of the Chicago phone directory. John Von Neumann came to rescue, by inventing in 1948 the first algorithm for automatic random number generation on the ENIAC, the “middle-square” method: his idea was to start with a number of n digits, square it, and retain the middle n digits of the result as the next random number. Such a method was quite poor, in that it invariably generates short-period repeats (start for example with 56: the squared sequence goes on as 562=3136, 132=169, 162=256, 252=625, 622=3844, 842=7056, 052=25, and you end up in a loop).
Notably, random numbers generated in digital computers can never be truly random, since the size of the word is necessarily finite. For a word of length L bits, no number larger than 2L –1 can be properly represented. Today’s computers typically use 64-bit words, so that the largest integer is 264–1, or something in the range of ~1019 different numbers. Random numbers generators display a cyclic recurrence with period equal to the largest integer, or some combination thereof, hence they are more properly called pseudo-random numbers. While 1019 looks like a pretty hefty quantity, it may be not enough for some critical applications, and even in standard computing there may be hidden surprises coming from the periodicity and clustering of pseudo-random numbers.
The main problem with algorithmic generators is the limited amount of entropy production. In the most common generators based on the “congruential” algorithm [ first proposed by DH Lehmer, Ann. Comp. Lab. Harvard Univ. 26, 141 (1951) ] the only source of entropy is the initial seed, after which the entire sequence is deterministically fixed, as Ron Harris knew well before spending seven years in a Federal prison.
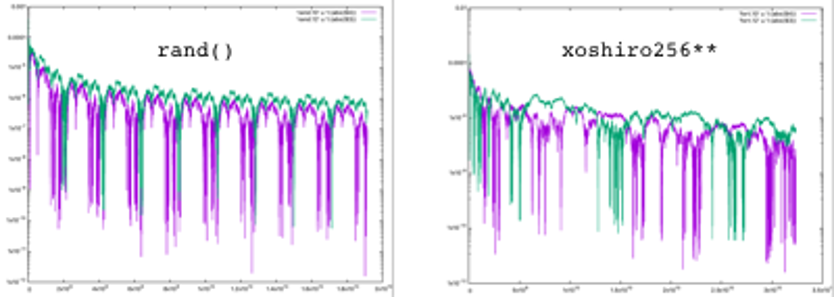
A way around is to make the sequence as long as possible, but it will never be infinite. The congruential algorithm makes use of the modulo operation on integers, generating a sequence x(n+1)=[a*x(n)+b]mod(c). What the modulo operation does is to round off the remainder of a division between the value of the argument (a*x(n)+b) and the largest integer possible. In 32-bit arithmetics, c=231–1, in 64-bits c=264–1, and so on. As a result, the sequence generated has a period of length c, as it can be easily verified on any personal computer. In the plot on the left of the figure enclosed, which I made for the joy of my few but highly esteemed readers, I represent the result of the deviation from the value 1/2, of the average (sum of all x(n) divided by n) for a sequence of 234 random numbers in [0,1] produced by the rand 32-bit function: the 231 periodicity is fully evident.
Smarter generators can have a period much longer than the largest integer, for example xoshiro256** [ from the family of shift-register algorithms by G. Marsaglia, J. Stat. Softw. 8, 14 (2003) ] has c=2256 –1: this sequence is truly humongous, and periodicity is not a real problem in practice: in the plot on the right, I used such a generator to produce a sequence of 235 numbers, and no periodicity seems to appear. However, it is not exempt from other issues, for example the clustering around particular values (it may produce a burst of numbers too close to 0 or to 1, breaking the homogeneity requirement at small scale), and the sequence can be inverted by particular multipliers, thus retrieving the original seed. In fact, both the congruential and the shift-register algorithms that we routinely use in our physics or chemistry Monte Carlo simulations, such as RANLUX or MIXMAX [ see: James & Moneta, Comp. Softw. Big Sci. 4, 2 (2020) ], are not considered “cryptography-safe” by the experts in computer security.
Random numbers are increasingly important to our digitally connected world, with applications that include e-commerce, cryptography, cloud computing, blockchain and e-currency, etc. Without knowing, each one of us is using random numbers every time we log in to a system or a webpage with a password. The authentication protocol takes your “human-readable” password and feeds it to a function called “hashing”, which generates a 128-bit output string (the “hash”) to be stored in the server. From this string it is virtually impossible to go back to the original password: if the server is attacked, hackers will obtain hashes, but not original passwords.
Producing a large amount of truly random numbers quickly, though, is a real-world challenge. The increasing demand to improve the security of digital information has shifted from sole reliance on pseudorandom algorithms, to the use of physical entropy sources. Ultrafast physical random number generators are key devices for achieving ultimate performance and reliability in communication and computation systems. And where else to search for physical randomness, if not quantum mechanics?
Semiconductor lasers featuring chaotic dynamics with tens-of-GHz bandwidth represent one prominent class of high-speed random number generators, can attain a frequency of 300 Gb/s [ I. Kanter et al., Nat. Photonics 4, 58 (2010)], and even more by coupling several lasers in cascade. However, the intrinsic time scales of lasing instabilities impose an ultimate limit on the entropy generation rate.
In the February 26, 2021, issue of Science a Yale-Dublin-Singapore team led by Professor Hui Cao (also a young French affiliate appears among the authors, S. Bittner, who was postdoc at Yale during this work) report the development of a compact laser that can produce random numbers at the spectacular rate of 250 Tbytes/second (note that today’s fastest CPU, the IBM zEC12, clocks at 5.5 GHz). They designed a special semiconductor shape to generate randomness. While previous devices relied on lasers’ chaotic temporal dynamics, Cao and her collaborators tailored their hourglass-shaped laser cavity to amplify many optical modes simultaneously; these modes interfere with each other to generate rapid intensity fluctuations; the lasing emission at one end of the device is imaged onto a streak camera that records the temporal fluctuation of the emission intensities at many spatial locations simultaneously; the fluctuations at different spatial locations are then digitized, to generate many random bit streams in parallel, which translate to random numbers. Quantum fluctuations make the bitstreams unpredictable, thus creating a massively parallel, ultrafast random bit generator.
The next step to make this technology ready for practical use now requires creating a compact chip, which incorporates both the laser and photodetectors. At that point, the random numbers could be fed directly into a computer (likely a massively parallel processor, such as a GPU), in a truly random sequence impossible to invert without violating the Second Law of thermodynamics.
