According to some unverified urban legend, in a sunny day of April 1954 the English physicist George Ingram Taylor was distractedly browsing a copy of the Life magazine that his wife had brought back from the beauty parlor, when he stumbled on a page reporting a series of photos of a huge white bubble expanding over a flat plain. He immediately recognized in those photos the streak camera images of the Trinity Test, the explosion of the first atomic bomb released in the Alamogordo desert on July 16, 1945. George gulped in consternation: that should have been still classified material, and the energy released by a fission bomb was a figure covered by the highest military secrecy. What if a copy of the magazine reached… Moscow…? (Actually, Taylor’s concerns, if true, would have been misplaced, since already in 1946 the Russian physicist Leonid Sedov had published a similar analysis of the shock wave, moreover with an exact analytical solution of the problem, and estimated that a large part of the energy would have been anyway dispersed as radiation.)
However, such a romanticized story is not quite realistic. In fact, Taylor himself revealed that in 1941 he had been approached by the UK Ministry of Home Security, who had learned that “it might be possible to produce a bomb in which a very large amount of energy would be released by nuclear fission”. The ministry wanted to know what the effects of such a bomb would be. Taylor (1886-1975) was one of the foremost English applied mathematicians of his day, and it was natural that the Ministry should seek his advice. He went to work on the problem, and approximated the solution with three differential equations and the Buckingham theorem of dimensional analysis. His work was not given clearance to publish until 1949, when it formed the first of two papers both titled “The formation of a blast wave by a very intense explosion”, appeared in the Proceedings of the Royal Society the next year. The first one simply reprinted the original report to the ministry, apart from the provision of a brief introduction, a few other minor changes and the addition of some supplementary material at the end. But such fine papers (and the similar works by Von Neumann and the already cited Sedov) were the product of theoretical considerations, without any support of experimental data (which would have remained scarce anyway, for quite a long time).
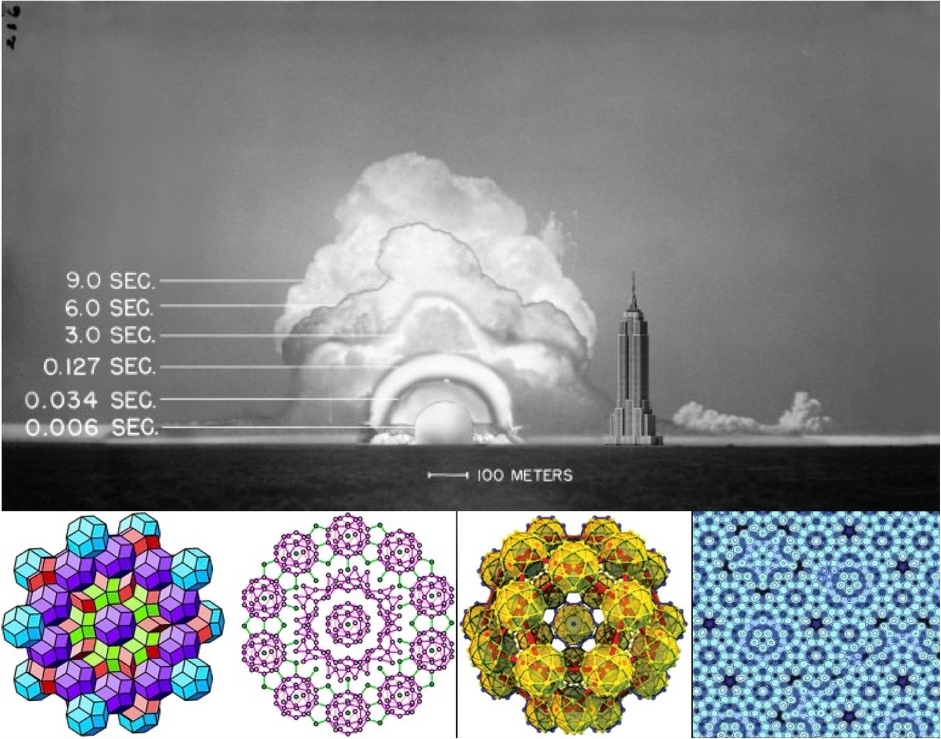
What happened with the photos published in Life is a different chapter of the story. Now Taylor (and the rest of the World) had access to real data. In particular, the photos reported the shape and size of the shock wave, from which a measure of the radius could be inferred, and a time stamp detailing the milliseconds each photo was taken after the blast. Then, the question becomes a “simple” matter of dimensional analysis (as you readers know, one of my dearest subjects) Considering that energy E has dimensions of [mass][length2][time-2], and the shock propagates in air with a density 𝝆, that has dimensions of [mass][length-3], it is easy to construct an equation for the growing radius of the wave as: R=Ex𝜌ytz.
Passing to the dimensional equation, we have [L]=[M]x[L]2x[T]-2x・M]y[L]-3y・[T]z . By equating the exponents of mass, length and time, it must be (x+y)=0, (2x–3y)=1, (-2x+z)=0, from which x=1/5, y=–1/5 and z=2/5. So, Taylor obtained an equation for the energy as a function of apparent radius and time that reads: E=C𝜌R5/t2, with C a constant that he assumed to be about 1 (a more accurate calculation gives a value for C=1.033). By plugging in the values fitted from the few photos, an estimate of about E=1021 erg, or 25 kilotons, is obtained, reasonably close to the measured value of 20,5 kilotons (and remembering Sedov’s note, that a large part of the energy would go into invisible radiation). However, also the whole story of the Life photos and the copy brought home by his wife is 100% fake news, and the result of a back-calculation: Taylor actually received the original photos of the Trinity test already a few days after the experiment in July 1945 (indeed, he was one of the few scientists invited to assist to the event in Alamogordo), and did this calculation immediately after, on the basis of the whole set of 25 images taken by the streak camera.
What makes the Trinity test, a story of 75 years ago, to come back with renewed interest is a work appeared in the May 17 issue of PNAS. The article is entitled Accidental synthesis of a previously unknown quasicrystal in the first atomic bomb test, co-signed by the well-known Paul Steinhardt from Princeton (if you dont’ know him, read below) and an equal share of scientists from University of Florence, Caltech, Los Alamos, University of Massachusetts, and by a private citizen living at 2702 Church Creek Lane in Edgewater, Maryland. As it turns out, part of the energy from the 1945 nuclear explosion went into the instantaneous fusion of the surrounding sand, the steel of the 30-m-high test tower, and the copper transmission lines, into a glassy material baptized as “trinitite”. This material is usually greenish in appearance, but the copper inclusions can make it reddish, here and there. Steinhardt, a theorist who made his fame by describing three-dimensional quasicrystals, guessed that red trinitite could be a good place to hunt for real quasicrystals, since these exotic structures often arise by combining materials that don’t go along together. After months of slicing, cutting and looking at SEM and x-ray patterns of mineral samples, they found a minuscule proof of a hitherto unknown composition of icosahedral quasicrystal, Si61Cu30Ca7Fe2. This represents the oldest man-made quasicrystal currently known, with the distinctive property that its precise time of creation is indelibly etched in history. The chemical dominance of silicon is evident, but Si in rocks is always found as a silicate oxidized form. Reducing silicon into a metallic alloy requires truly extreme conditions, such as the intense heat and pressure of the nuclear shockwave.
Quasicrystals are a rara avis, rare birds. In short, they can be described as regular crystal structures that lack translational symmetry. The first example was spotted by Dan Shechtman and coworkers, in a rather inconspicuous 1984 PRL paper, A metallic phase with long-range orientational order and no translational symmetry, which however 27 years later brought him the Nobel prize in chemistry. (The last signataire of the paper was the marvelous John Cahn: again, one wonders why Shechtman got the prize and not Cahn, whose contribution to materials science has been paramount?) Shechtman had observed a 10-fold symmetry in the diffraction pattern of a sample cast from a liquid Al-Mn alloy. For more than 10 years, the idea of quasicrystals was strongly opposed, with Linus Pauling as one of the strongest critics (“There is no such thing as quasicrystals, only quasi-scientists”). Two-dimensional non-periodic tilings of the euclidean plane had been studied in the ’70s by Penrose and Conway, based on some earlier ideas going back even to the renaissance artist Albrecht Durer. It was the crystallographer A. L. Mackay who, in 1982, suggested that the Fourier transform of a Penrose tiling would show fivefold symmetry (Bravais crystals, as you know, can only have three-, four- or sixfold symmetry), thus indicating a practical way to identify such “quasi-crystals”, in case you would meet one. After Shechtman work, however, such identifications were all but rarissime, and required smashing metal powders in high-energy ball mills, or ultrarapid quenching from molten metals. The first and only natural example of quasicrystal, the “icosahedrite”, was found only in 2009 (https://doi.org/10.1126/science.1170827) by the same Paul Steinhardt who now just found the quasicrystal structure in the remains of the Alamogordo nuclear explosion. As Steinhardt describes in his book The second kind of impossible, that unique finding was the result of an Indiana-Jones-like quest in the Koryak mountains of Eastern Siberia, Russia, where they found the icosahedral structure hidden in the crystalline Cu-Al alloys from a meteorite. They made the hypothesis that this exotic quasicrystal was probably formed in a collision between two asteroids in the early Solar System, in which energies comparables to a nuclear explosion could occur.
As it stands, quasicrystals have no known use or practical application to date. However, the mathematics behind them is amusing. Finding rules for arranging a structure that has local order and long range symmetry but never repeats itself, is one of those intellectual challenges that may keep one’s mind busy for years, as Alexey Madison from St Petersburg can testify. His models for stacking of quasi-unit cells to obtain quasi-periodic structures of quasi-crystals are quasi-fantastic (see e.g., https://doi.org/10.1039/C5RA13874D or https://doi.org/10.1098/rspa.2018.0667). In their endeavors, quasi-crystallographers have used a variety of mathematically sophisticated but physically unrealistic models. I am running short of space, and cannot go on describing how Durer had already invented in 1525 a pentagonal tiling of the plane with ten symmetry axes and a golden ratio between the lengths of the sides, and how such a fivefold tiling is observed in the structure of some viral capsids… For me, just the beauty of looking at a diffraction pattern with symmetric spots arranged by groups of ten already represents a subtle pleasure.
