Unlike animals, which generally have to contend with a body plan which is fixed at birth, plants can continue to develop new organs and elaborate their body plan throughout their life. A beautiful example of a nearly regular and periodic patterns is the spacing of leaves, called phyllotaxis. Such observations had been fascinating philosophers and scientists as far back as Theophrastus, with his Historia plantarum in the III century BC, and Plinius, with his Naturalis historia in the I century. Leonardo Da Vinci in the mid-XVI century described the spiral patterns of plants, and Johannes Kepler in the beginning of the XVII century was likely the first to conjecture that Fibonacci numbers were somehow involved in the structure and growth of plants. About 1836, the Franco-German botanist Wilhelm Philippe Schimper observed that after some number of complete turns around the stem of a plant, another leaf would lie almost directly above the first. He gave the name of divergence angle to the number of turns divided by the number of leaves in a cycle. The brothers Auguste and Louis Bravais (the first was the famous crystallographer, the second a physician passionate of botany) observed that this angle is close to 2𝜋/𝜑 radians in most plants, or 137.5 deg, where 𝜑=(1+√5)/2 =1.61803…, is the Sectio aurea, or “golden mean”.
Such regularities, or near-regularities, are indeed commonplace in the plants’ world: for example, the stalks or florets of a plant lie along intersecting spirals running clockwise and counter-clockwise. In a famous 1953 paper [Golden mean, phyllotaxis and Wythoff’s game, Scripta Math. 19(2,3)], the British-Canadian geometer and musician Harold Coxeter described the arrangement of scales on the surface of the pineapple fruit in terms of families of intersecting spirals. Actually, what we call pineapple is the result of the progressive fusion of many flowers, germinating from a common stem and growing on top of each other, over a long time ranging from several months to about 3 years. By accurately numbering the scales on the pineapple skin, Coxeter identified three series of spirals, starting invariably at positions 5, 8 and 13 with respect to an arbitrary zero. The three numbers belong to a famous series that the medieval Italian mathematician Leonardo Fibonacci described in his Liber abaci of 1202, but which was already known to Indian mathematicians from centuries before. As you know, the series is also intimately related to the golden mean, since the ratio between any two adjacent numbers in the series represent increasingly good approximations to 𝜑.
Similar spiral arrangements are widespread observed in fruits and flowers, such as the arrangement of scales in pine cones, the surface of douglas fir branches, thistle inflorescences, sunflower heads, cactus ridges, and so on. The parallel sequences of equivalent spirals are called parastychies, and their number is often one from the Fibonacci series. Many other such regularities, more often pseudo-regularities, can be discovered among plants, probably owing to the more static structures of the almost immobile vegetables, when compared to the dynamical structures of moving animals. For example, by looking at the stalks of a celery in cross section, some have observed that the (approximate) projection of the (approximate) centre of mass of each successive stalk n is placed at a position that (approximately) corresponds to the spacing of the points 2𝜋n/𝜑 on the unit circle. Such elegant calculation about a (vaguely defined) stalk’s centre of mass, leads such curious observers to claims such that “stalks are optimally spaced”, and “the golden-mean angles ensure that successive stalks are inserted where they have most room”.
Both mathematicians and laymen are fascinated by these recurrent numerical patterns, which however are only approximate in practice, and unfortunately quite less stringent than one would love to see. This could be dubbed as a very typical case of Platonism in science, in that the beauty of an idea takes over its scientific basis, in some extreme cases up to the point of forcing will against evidence. However, besides such fuzzy concepts of “regularity” and “beauty”, the really big and even more interesting question is: what are the physical, chemical and biological origins of such patterns? There are currently two major approaches for the explanation of phyllotaxis, both put forward at the beginning of the XX century. A first approach (G. van Iterson, Mathematische und mikroskopisch-anatomische Studien über Blattstellungen, Fischer, Jena, 1907) supposes that leaf primordia are formed at the “first available space”. Such model, complemented by the idea of a contact pressure providing a physical basis to the observation of space-filling patterns (I. Adler, A model of contact pressure in phyllotaxis, J. Theor. Biol. 45,1 (1974)), was formalised in a “fundamental theorem of phyllotaxis” that should enable to recognise and classify patterns into mathematical objects. On the other hand, many more experiments appear to support instead a second approach, which assumes a field of inhibition around each existing primordium, such that new primordia should form where the total inhibitory influence is least (J. C. Schoute, Beiträge zur Blattstellung, Rec.Trav. Bot. Neerl. 10, 153 (1913)). This idea, amazingly outlined half a century before Turing’s seminal work on morphogens, exactly summarises the behaviour of the activator-inhibitor model (A. M. Turing, The chemical basis of morphogenesis, Phil. Trans. Roy. Soc. B237, 37 (1952); it is my opinion that just this only work could have justified a Nobel prize to Turing).
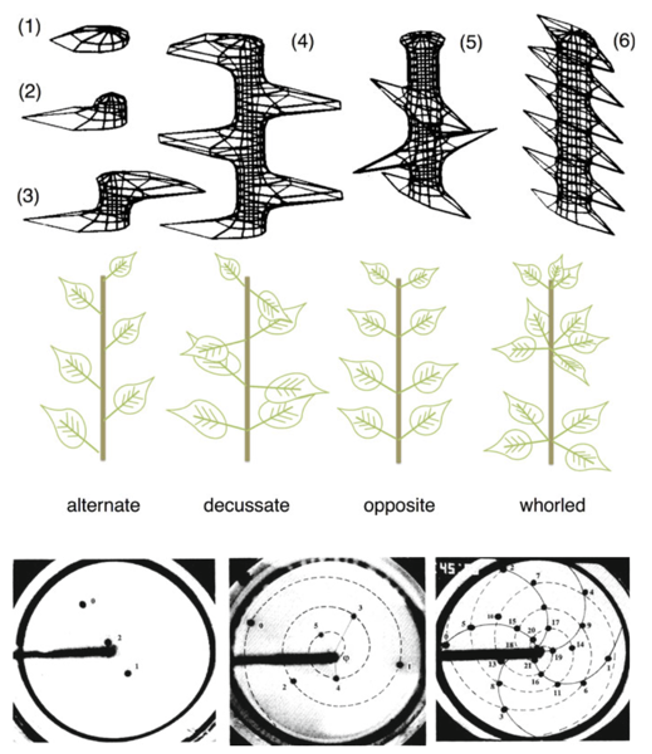
The a–h model was used by H. Meinhardt in computer simulations of a growing shoot, approximated as a cylinder (Models of Biological Pattern Formation, Academic Press, London, 1982). In the model, plant cells are doubled at fixed time intervals starting at one end of the cylinder, with a random fluctuation determining the location of the first maximum. This gives the position of a first leaf, and at the same time produces an inhibitor field that blocks the formation of other leaves in the immediate neighbourhood (see enclosed figure, top, 1-3). After further cell growth, the next maximum appears, e.g. on the opposite side of the cylinder, thus originating the alternate leaf pattern. Depending on the precise values of the model parameters, various other leaf patterns can emerge: for example, the spiral (or decussate) pattern can be formed if the diameter of the stem is larger than the diffusion range of the inhibitor, especially if an inhibitory influence from the apex prevents new leaves from arising near the apex itself (see enclosed figure, top 4-6, and middle).
The spiral arrangement of leaves and inflorescences, and the Fibonacci series that invariably appears in such cases, can also be explained on the basis of models including lateral inhibition with the proper geometrical constraints. Going into a spiral pattern becomes somewhat obvious, when you are a leaf and must be born out of a central stem. To avoid crowding, leaves and flowers must necessarily sprout at some angle from the preceding ones. If this angle is nearly constant, which amounts to say that the time between the birth of each new leaf or new flower is approximately constant, a few spirals will result, when looking from above down the plant stem. This is just the previously introduced “divergence angle”, whose value may be obtained from the requirement of optimally filling the space, while leaving as little voids as possible. In some cases, a generous approximation may show Fibonacci numbers to appear out of geometric spirals. But then, can we give a more physically-grounded reason for the appearance of Fibonacci numbers, besides the purely geometrical constraint of space filling?
A series of experiments of beautiful simplicity carried out in 1992 by Stéphane Douady and Yves Couder, both at the Ecole Normale in Paris at that time (Phyllotaxis as a physical self-organized growth process, PRL 68, 2098), demonstrated that the growth process from a central stem, typical of the plant world, may approach the Fibonacci-like patterns because of spontaneous self-organisation into structures that satisfy the best space-filling constraints. However, they used something as far away from a plant as you can imagine: magnetic beads falling on a rotating oil surface. The circular border of the surface is magnetised, such that droplets separated by a distance d repel each other, with a force proportional to d-4, and stream toward the outer border at a steady velocity v limited by the viscosity of the oil. The physics of the process is governed by the single nondimensional parameter G = vT/r, product of the velocity times the dripping period T, and divided by the radius r of the circle. A value of G close to 1 (in scaled units) means that the system is dominated by the radial velocity: droplets move quickly away from each other along opposite directions, simulating the case of a very short-lived inhibitor repulsive field. For smaller values of G the mutual repulsion is increasingly long-lived; at G ≃ 0.7, droplets break the 2𝜋 symmetry and start to take a spiral pattern; at even smaller values G ≃ 0.15, more spirals are formed and the divergence angle increasingly approaches the “golden” value of 137,5 deg (see enclosed figure, bottom). In the same experiments, it was shown that the convergence to Fibonacci-like patterns is independent of the value of the repulsive force, in that also forces different from the d-4 law will end up in the same qualitative results.
I leave it to your own imagination to consider whether this should be a magical or mysterious coincidence, or rather just one of the many emergent phenomena that arise everywhere in Nature, because of the cooperative action of so many agents. However, space filling is one but not the only requirement that plants try to satisfy during their growth. Other concurrent factors could be the availability of sunlight, the proximity of other plants, the presence of obstacles that flow water asymmetrically around the stalk, and many others. As a result, such regularities can only be observed on average, to the dismal of the Platonists out there. The next time you go for a walk in the garden, it will be a pleasant challenge trying to find how many flowers respect the Fibonacci numbers with their petal crowns… but take into account that many petals and leafs could have gone lost, maybe because of wind, rain, insects, or of other walkers less attentive than you!
