What do Euclid, a twelve-years-old Einstein, and former American president James Garfield have in common? They all came up with elegant proofs of the famous Pythagorean theorem, one of the most fundamental rules of geometry and the basis for innumerable practical applications, from constructing a stable for animals, to calculating terrestrial coordinates from GPS data. Actually, the theorem is ascribed and named after the Greek genius of 6th century BC, but its essence had been known from thousands of years before. A Babylonian tablet from about 1,800 BC lists fifteen sets of triplets that clearly satisfy the theorem, like 120,119, 169; 3456, 3367, 4825; 4800, 4601, 6649; and so on. Historians of architecture compellingly show that Egyptians used the 3-4-5 rule to obtain square corners in their constructions. Their “demonstration” makes use of a piece of rope with 12 equally spaced knots that, once folded into a triangle with sides made of 3, 4 and 5 knots, results in a nice 90-degrees corner. Moreover, the earliest known Indian mathematical text, written between years 800 and 600 BC, already stated that “a rope stretched across the diagonal of a square produces a square that is twice the original” (mind my Sanskrit translation!).
The importance of the “theorem” of course lies in its ability to convince our brains that such a bold statement as a2+b2=c2 holds for any right triangle on a flat surface, and not just for the examples above, listed one after another. It gives what we call a “proof” that the statement is universal and independent on each own’s measurements or calculations. A proof starts from a set of rules and follows a strictly binary logic in which such rules are applied sequentially, to obtain the desired result. If you accept the premises fixed by the rules and adhere to the binary logic, then the result must be valid everywhere and at all times. This feature is a peculiarity of Ancient Greece mathematics, something that apparently escaped the analogic reasoning of earlier peoples, like Egyptians or Babylonians, whose mathematical statements were produced on a case by case basis (hence the need to compile endless “lists” of cases for which a given relationship holds, instead of writing down a single, concise formula). For those of you (like me) interested in such questions, today’s reading suggestion is the classic 1949 book by Otto Neugebauer, The Exact Sciences in Antiquity (you can easily find the Dover reprint).
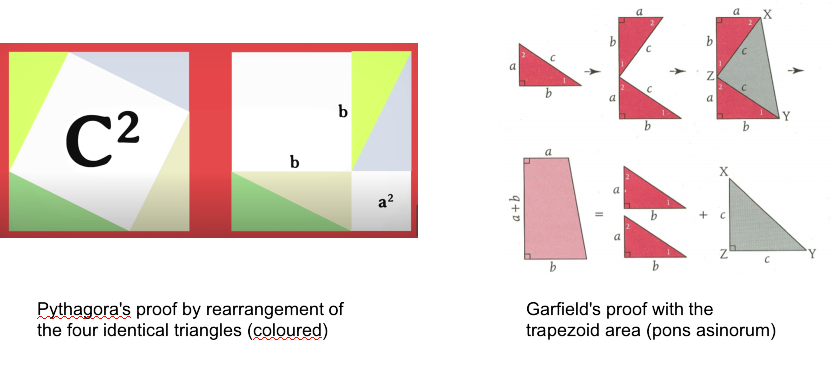
Pythagoras’ proof (shown in the figure above) uses a classic strategy called “rearrangement”. You start with four identical right triangles whose sides are all equal to a and b, and hypothenuse c. Then, rotate them to form a geometrical figure of a square whose four sides coincide with the four hypothenuses. This square, with area equal to c2, looks somewhat tilted and inscribed in a larger square, whose sides are each equal to (a+b). Now, the proof is obtained by shifting the four identical triangles inside this new, large square, to compose two rectangles (see the enclosed figure, left) that now delimit two smaller squares of area respectively a2 and b2. Since the area of the large square minus the four triangles is always the same, the construction implies that a2+b2=c2.
Euclid provided a different proof, which was also stumbled upon about 2,000 years later by somebody else. This proof takes a large, right triangle, and divides it into two smaller ones by a segment perpendicular to the hypothenuse. By using the laws of similarity of angles, the angles of all these triangles must be the same, hence their sides must be proportional to each other. A simple rearrangement of the terms of proportionality between the paired sides gives the Euclidean proof, that was independently “rediscovered” by the somebody else in the year 1891: a 12-years old kid playing with geometrical figures in his room in Ulm, Southern Germany, named Albert Einstein.
As far as General James A. Garfield, at the time a representative of the U.S. Congress for Ohio who was to become the 20th president in 1881 (that is before becoming the second president to be shot, in the list of four), he published in 1876 New England Journal of Education (vol.3 n.14) a proof known as pons asinorum (Latin for “the bridge for donkeys”). This proof (shown in the right figure above) starts with a diagram of a trapezoid with bases a and b, and height (a+b). The area of the diagram can be ascertained in two different ways: as that of a trapezoid, and as that of three right triangles, two of which are congruent (see enclosed figure, right), and the proof follows by equating the sum of areas. As of today, more than 350 different proofs of Pythagoras’ theorem are known, some of them very funny such as the “tiling proof”, in which the infinite plane is tiled with irregular triangular and quadrangular figures whose sums of areas gives the theorem; or the “mechanical” one, in which the theorem is proved by filling square buckets with water.
By now, you could be convinced that the axiomatic approach of Greek mathematics was so much superior to the more ancient ways of reasoning, from Egyptians or Babylonians, up to completely discredit the discoveries of these latter as the result of mere chance, or coincidences. On the other hand, the ancient people had their brains identical to Greeks’, and used the same binary logic that is apparently engrained in our minds (see a famous study by neurophysiologist Joe Tsien, Frontiers Neural Circ. 2016). So, why they would not use the more powerful deductive reasoning, instead of inductive fact checking? We are pretty sure that our human brain did not evolve substantially in its build, since at least the late Paleolithic. However, the progress in reasoning abilities clearly demonstrates a rapid change over the last few thousand years, and how it happened remains still a mystery. Which does not, however, allow to rule out the pre-Greek science as just a kind of babbling garbage, none the least because we have for these sources much less easily accessible documents, compared to the ample written heritage of classic Greece.
I hope then to surprise you with the finding that a piece of clay, a flat tablet about 4×4 cm in size, carved by a Babylonian astronomer around year 300 BC, contains the proof that ancient Babylonians used a complex geometrical model, something that looks like a rudimentary form of integral calculus, to calculate and predict the path of Jupiter. While it was thought that mathematical techniques of this kind would have to wait until medieval Europe to be invented, the discovery attaches a whole new meaning to ancient astronomy. As discussed above, Babylonian scholars were thought to compute only with sequences of numbers, and yet this tablet plots the apparent velocity of Jupiter from the planet’s first appearance along the horizon, to 60 days later, and then 120 days later. If drawn on a graph, this relationship is represented in the shape of two conjoined trapezoids. As it turns out, the area of each trapezoid describes Jupiter’s total displacement (measured in degrees) along the ecliptic, or the path of the sun.
The scientist who made this amazing discovery is Mathieu Ossendrijver, both an Assyriologist and astrophysicist now at Freie Universitaet in Berlin (see Science vol.351 p.482, 2016). In his words, the tablet reports “not an actual trapezoid, such as describing the shape of a field or some observable configuration of the planets in space. It is a configuration in a mathematical space, a highly abstract application.” Greek astronomers around the same time, such as Ptolemy (who was in fact Egyptian by birth) used geometry to make calculations in the real 3D space, such as using circles to represent the orbits of planets around the Earth. With all their axiomatic reasoning, however, the abstract use of geometry was unheard of at that time, notably the abstract description of bodily motion in time and space. Historically, time charts are known to have been invented in Oxford, in the 14th century, with the “Merton speed theorem” which calculates the average velocity to cover a same displacement corresponding to an accelerated motion. This allows to calculate a displacement as the area under a plot of velocity vs time. Just 1,800 years earlier, Babylonians had their own technique to predict planetary motion based on the same integral principle.
Ossendrijver’s tablet is part of a group of four from the British Museum collection, which have been puzzling historians of science since the second half of the XIX century. In fact, these four tablets excavated in ancient Iraq, appeared to mention computations with trapezoids, even though the Babylonians had never been known to use geometry in their calculations. Yet, the tablet text points clearly to a geometric understanding, not just a geometric representation of how Jupiter moves in the sky, but a geometric technique allowing to track and predict its motion over time. The newly deciphered tablet was the missing piece in the puzzle. The year before, a colleague had handed Ossendrijver a pile of photographs, including an image of a tablet he had never seen before in the British Museum. A few months later, Ossendrijver went to London to hold it in his hand and read it himself, confirming what he already suspected the calculations describe.
Jupiter motion along the ecliptic is described in the Babylonian tablet in terms of its daily displacement, with segments corresponding to piecewise different velocities, from its first appearance to the first station, at which the apparent retrograde motion begins, and back up to its disappearance below the horizon. In a velocity vs time representation, the trajectory is represented by trapezoids, whose areas give the total displacement.Reading the original Science paper by Ossendrijver is a great fun, in trying to repeat the ingenious calculations. For our own sake, the good Mathieu has also included in the Supplementary Materials the Latin transliteration of the Assyrian text, together with a proper English translation. You can find it here:
https://www.science.org/doi/suppl/10.1126/science.aad8085/suppl_file/ossendrijver.sm.pdf
Out of sheer curiosity, the Assyrian word for “trapezoid” seems to be SAG.KI, with the prefix SAG meaning “side”. Now you know it.
